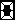∫[0→1]e^x│x-a│dxの値を最小にするaの値を求めよ。(東京工業大学)で
積分の範囲の質問です。(計算はしなくて結構です。aの範囲だけ質問です)
◎ 1つめの質問
(あ)は正しいく参考書では(い)が誤りと書いてありました。
しかし別の参考書では(い)が書いてありました。(い)は誤りですか。
(あ)a≦0 のとき f(a)=∫[0→1]e^x(x-a)dx
0≦a≦1 のとき f(a)=-∫[0→a]e^x(x-a)dx+∫[a→1]e^x(x-a)dx
1≦a のとき f(a)=-∫[0→1]e^x(x-a)dx
(い)a≦0 のとき f(a)=∫[0→1]e^x(x-a)dx
0<a<1 のとき f(a)=-∫[0→a]e^x(x-a)dx+∫[a→1]e^x(x-a)dx
1≦a のとき f(a)=-∫[0→1]e^x(x-a)dx
◎ 2つめの質問
「f'(a)を求めるときに、一般にa=0,1は微分可能でないので(この問題ではa=0,1は微分可能)
以下のようにaの範囲を分ける。
a<0 のとき f'(a)=-(e-1)
0<a<1 のとき f'(a)=2e^a-(e+1)
1<a のとき f'(a)=e-1 」
と書いてありました。
a=0,1は微分可能でないときは「a≦0,0<a<1,1≦a」にしない方がいいですか。
|
No.89759 - 2025/01/14(Tue) 13:36:10
| ☆ Re: 積分、微分の範囲の質問 / てつや | | | ◎ 1つめの質問でf(a)で「a≦0,0<a<1,1≦a」にしてはいけない(「a≦0,0≦a≦1,1≦a」)にする理由は添付の通りです。
157ページの補足1に書いてある通りで、図の2行上と一番下のように、
「もし、関数f(a)がa=0,a=1でともに連続であることがいえなければ、〜〔解答〕において、□(参考書では赤い□です)の部分にすべて等号を入れないと、右図のような可能性を排除していないので誤りとなる」と述べられています。
このように「a≦0,0<a<1,1≦a」は誤りで、「a≦0,0≦a≦1,1≦a」にする必要があると述べています。
しかし、他の参考書では「a≦0,0<a<1,1≦a」になっています。どちらの参考書が正しいのですか。
|
No.89769 - 2025/01/15(Wed) 08:33:17 |
| ☆ Re: 積分、微分の範囲の質問 NEW / 黄桃 | | | 既に述べたとおりです。
この問題のポイントの1つはa=0,1でf(a)が連続であることを利用して議論することでしょうから、そこに抜けがあれば誤りとされる、ということです。
別の言い方をすれば、f(a)がa=0,1で連続、ということをきちんと記述し、議論を進めていけば「a≦0,0<a<1,1≦a」で構いません
(例えば、f(a)はa=0で連続で、a=0の近くでは単調減少だから、0<a<m (mは0<a<1での極小値をとるaの値)でf(0)>f(a)である、
などと記述する。a=1も同様) 。
そうした記述なしに、「a≦0,0<a<1,1≦a」で場合分けして、機械的に各区間の増減を調べるだけの議論をしてしまうと誤りとされる、ということです。
個人的には、「a≦0,0≦a≦1,1≦a」で場合分けすれば後は、機械的に各区間の増減を調べるだけの議論をしたらそれでOK,とは思わないですが
(なぜ、このようにa=0,1が両方に含まれて矛盾がないのか、を一言説明する必要がある;つまりa=0,1でのf(a)の連続性を明示的に示す必要がある)、
この参考書はf(a)のa=0,1での連続性は自明だから明示的に説明する必要はない、としているようです。
東工大レベルの問題なら、単純に「a≦0,0<a<1,1≦a」か「a≦0,0≦a≦1,1≦a」の2者択一で判断するのではなく、自分の頭で考えて判断しましょう。
#理解できなくても点数を取れるようにする(≒売れる参考書にする)にはこう書くのがいいのでしょう。
|
No.89773 - 2025/01/16(Thu) 06:42:39 |
|