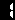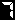解答を確認していただきたいです。
![]() |
No.87849 - 2024/04/03(Wed) 14:58:25
| ☆ Re: 複素数 / ast | | | > 問題文はこれで全てです
問題文が "原点を通らない直線" としか述べない (出題者は解答者にはそれだけで伝わるようにあらかじめ教材全体を組み立てているつもりでいる&実際におそらくそうなってる) からこそ, わたしは「問題文」ではなく「文脈」(前後のあるいは解説・模範解答等の文章, ほかの問題や, そもそもその単元の内容, 特にその数学的対象の記述等の扱い方)がどうなってるのかの話をしてる.
# こっちは記述の仕方の例まで挙げているのに, 教材のそれらしい部分にあたるどころか
# まだ「問題文」だけしか頭にないというのでは困る.
他の質問の問題文も再度確認してきたが, あるいは質問者がたとえば円を表すのに |z-α|=r (α:複素数, r>0:実数) の形式を頑なに使わないで x^2+y^2=r^2 のような形式を専ら使うなどを鑑みるに, 直線は「z=x+yi (x,y:実数) としたとき x,y が ax+by+c=0 (a,b,c:実数) を満たす」といった形でその資料のその単元では扱ってるのではないの?
> 解答を教えて
このように話の出発点 (No.87857 のように L:z=(t-1)α+tβ とおいてよいのか, あるいはいま述べたように L: z=x+yi where ax+by+c=0 とおいてよいのか, あるいはもっとほかの形が適正として扱われていてそうでなければ不適切とされてしまうのか etc.) がいくつも考えられてあまりにも不明瞭だから論理的にムリと言ってる. あなたがこの点を解決するのが絶対の大前提.
|
No.87859 - 2024/04/03(Wed) 22:54:44 |
| ☆ Re: 複素数 / ast | | | まあいいや, 直線を仮に z=x+yi, ax+by+c=0 から始めてよいなら, 「これは二点 (-c/a,0),(0,-c/b) を通るから α:=-c/a, β:-ci/b とおけばこの直線は z=α+t(β-α) (t:実数) とも書けて t=(β-α)/(z-α) が実数 ⇔ (β-α)/(z-α)=((β-α)/(z-α))^- ⇔ (α-β)^- z + (β-α)z^- = -2iIm(αβ^-). (ただし, 複素数 ω に対して, ω^- は ω の複素共軛, Im(ω) は ω の虚部)
だから w:=(i(β-α))^-/(2Im(αβ^-))=(-a+bi)/(2c) ととればよい.」みたいなことをやることになる.
# 計算はいまざっとやっただけで確かめてない (たぶんちょこちょこ間違ってる) し,
# 直線だから "a,b の何れかは 0 でない" とか, ab=0 のときは別に調べるとかもあるだろうが,
# こっちでそれらを細かくケアしたとて, そもそも出発点がちがってるならどうせ無意味にしかならんので,
# そういうのは文脈の確認含めてそっちでやって).
|
No.87860 - 2024/04/03(Wed) 23:40:03 |
|