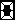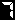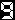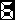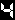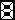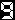n 1
Σ ーーー
k=1 k(k+2)
を部分分数分解して
1 1 1
ー (ーーー - ーーー)となり、
2 k k+2
1から代入していくと隣の項ずつ消えず、一つ飛ばしで消えていきますが、最終的にそれを一般項として扱えるのかどうしても理解できません。
その公式に、1、や2を代入した時にもちゃんと成立するのは分かります。ですが、なぜ一個飛ばしで変形という形で求めた一般項が1、2を入れてもちゃんと成立できてしまうのか、分からないのです。このような場合の部分分数分解の理解においてどこか大事な部分を見落としているような気がします。
分かりづらい説明で申し訳ございません。
|
No.87923 - 2024/04/26(Fri) 04:59:16
| ☆ Re: 隣の項の消えないシグマの部分分数分解について NEW / ast | | | 疑問のありかがよくわからないのですが, Σ-記法を用いずに "+" だけで書くとどんな項が出てきて, どの項とどの項がどのように打ち消し合うのか, それを具体的に書き下せますか? あるいは書き下したとして,
Σ_[k=1,…,n] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)+…+(1/n-1/(n+2))
= (1/2)(1/1+1/2+1/3+1/4+1/5+……+1/n)
-(1/2)( 1/3+1/4+1/5+……+1/n+1/(n+1)+1/(n+2))
= (1/2)(1/1+1/2 - (1/(n+1)+1/(n+2)))
の具体的にどの項があなたがおかしいと感じる部分ですか?
# (具体的過ぎる例では余計な要素が見えすぎて気を逸らしてしかねないので) もう少し抽象化するけれど,
少なくとも
(i): 数列 {a[n]} が別の数列 {α[n]} を使って a[n]=α[n]-α[n+1] と書けるならば
Σ_[k=1,…,n] a[n] = α[1] - α[n+1].
であることが本当にわかっているのであれば, 一般に
(ii): 数列 {b[n]} が別の数列 {β[n]} を使って b[n]=β[n]-β[n+2] と書けるならば
Σ_[k=1,…,n] b[n] = (β[1]+β[2]) - (β[n+1]+β[n+2]),
(iii): 数列 {c[n]} が別の数列 {γ[n]} を使って c[n]=γ[n]-γ[n+3] と書けるならば
Σ_[k=1,…,n] c[n] = (γ[1]+γ[2]+γ[3]) - (γ[n+1]+γ[n+2]+γ[n+3]),
(iv): 数列 {d[n]} が別の数列 {δ[n]} を使って d[n]=δ[n]-δ[n+4] と書けるならば
Σ_[k=1,…,n] d[n] = (δ[1]+δ[2]+δ[3]+δ[4]) - (δ[n+1]+δ[n+2]+δ[n+3]+δ[n+4]),
…… etc.
もすべて全く同じ理屈 (何と何とがどう打ち消し合っていて, 何が残るのか) で言えること
# むろん, 本問においては,
# a[n]=1/(n(n+1)), b[n]=1/(n(n+2)), c[n]=1/(n(n+3)), d[n]=1/(n(n+4)), ……
# α[n]=1/n, β[n]=(1/2)(1/n), γ[n]=(1/3)(1/n), δ[n]=(1/4)(1/n), ……
# だと思って読めばよいが.
なので, こちらとしてまず気になることは
> 隣の項ずつ消え
の場合 (つまり (i)) もそもそもきちんと理解していないのでは, というところですね.
# (i) では "隣り合う項を k を 1 ずつ増やしながら消していく" ところ, 例えば
# (ii) では "打ち消し合う項は「一つ飛ばし」だが, そのために辿る k は 1 ずつ増えることに変わりない"
# といったあたりで,
# 例えば「一つ飛ばし」などの標語的な言葉に安直に流れて, 複数の異なる要素に妙な混同をするような
# 自縄自縛に陥らずに, 既知の例をきちんと敷衍できるかというようなところまでいって
# ようやくここで私が言うところの「きちんと理解」の範疇といえるところかと.
> それを一般項として扱える
は意味が分かりません, 単に (k=1 から k=n までの) 和を計算する (と n が残る) だけで一般項もくそも別段かかわりない話ではないですか?
# つまり, もし仮に「数列 {a[n]} から S[n]=a[1]+a[2]+…+a[n] で新しい数列 {S[n]} を作ったら
# {S[n]} の一般項 S[n] が n の式になった」という話なのであれば, そらあたりまえだろう, と.
|
No.87927 - 2024/04/26(Fri) 10:51:05 |
| ☆ Re: 隣の項の消えないシグマの部分分数分解について NEW / ast | | | ## 書いてる途中で返答があったようなので齟齬はあるだろうけれどそのままレスします:
# これはそもそも「Σ を何だと捉えている」と問うべきだろうか?
n=1,2 のときの和
Σ_[k=1] (1/2)(1/k-1/(k+2)) = (1/2)(1/1-1/3)
Σ_[k=1,2] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)
にどんな「物凄い違和感」があるのかなるべく具体的に説明してみてくれますか? あるいは
Σ_[k=1,2,3] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)+(1/3-1/5)),
Σ_[k=1,2,3,4] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)+(1/3-1/5)+(1/4-1/5)),
……
Σ_[k=1,2,…,m] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)+…+(1/m-1/(m+2)), (ただし m は 1<m<n)
Σ_[k=1,2,…,n] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)+…+(1/n-1/(n+2))
とすべて書き並べた場合, 物凄い違和感はどこかで薄れますか? もしくはどこまで物凄い違和感を覚えますか?
違和感が残るのであれば具体的にそれはどのような違和感ですか?
> そもそもn番目までの和を求める、と言われている問題では、
そういう問題において「n は (任意の値の) 定数」(n の具体的な値を解答者は知ることはできないが, 問題の最初から最後まで同じ一つの値であり続けるもの) ですよ.
# それでたとえ出題者が n がどんな値だと開示しても, それで正解不正解が変わったりしない答案を
# 文字のまま n を使って書くというのが趣旨.
## そしてそれは「一般項」(n が自然数値を亘る変数) の話ではない.
|
No.87933 - 2024/04/26(Fri) 13:11:12 |
| ☆ Re: 隣の項の消えないシグマの部分分数分解について NEW / あ | | | > # これはそもそも「Σ を何だと捉えている」と問うべきだろうか?
> n=1,2 のときの和
> Σ_[k=1] (1/2)(1/k-1/(k+2)) = (1/2)(1/1-1/3)
> Σ_[k=1,2] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)
>
> にどんな「物凄い違和感」があるのかなるべく具体的に説明してみてくれますか? あるいは
> Σ_[k=1,2,3] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)+(1/3-1/5)),
> Σ_[k=1,2,3,4] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)+(1/3-1/5)+(1/4-1/5)),
> ……
> Σ_[k=1,2,…,m] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)+…+(1/m-1/(m+2)), (ただし m は 1<m<n)
> Σ_[k=1,2,…,n] (1/2)(1/k-1/(k+2)) = (1/2)((1/1-1/3)+(1/2-1/4)+…+(1/n-1/(n+2))
> とすべて書き並べた場合, 物凄い違和感はどこかで薄れますか? もしくはどこまで物凄い違和感を覚えますか?
> 違和感が残るのであれば具体的にそれはどのような違和感ですか?
>
いえ、こう見ると物凄く分かります。
1を入れても、成立している。
2を入れても、成立している。
3を入れても、成立している。
これを見ると隣り合う項ずつ消えるかどうかは、どうでもいいことなのだと思います。
上手く言えないことが悔しいのですが、
強いて言えば、なぜ成立するのか、ということを言いたいのかもしれません。痒いところに手が届かないような感じです。
> > そもそもn番目までの和を求める、と言われている問題では、
> そういう問題において「n は (任意の値の) 定数」(n の具体的な値を解答者は知ることはできないが, 問題の最初から最後まで同じ一つの値であり続けるもの) ですよ.
> # それでたとえ出題者が n がどんな値だと開示しても, それで正解不正解が変わったりしない答案を
> # 文字のまま n を使って書くというのが趣旨.
> ## そしてそれは「一般項」(n が自然数値を亘る変数) の話ではない.
ありがとうございます。ここは理解できました。
|
No.87936 - 2024/04/26(Fri) 13:24:36 |
| ☆ Re: 隣の項の消えないシグマの部分分数分解について NEW / ast | | | ### もう解決したようで蛇足になりますが, せっかくなので書いていた補足を投げておきます.
# 何となく想定していた内容はあって, だいぶ近い返答まで来たので,
# 当初の想定でよかったのだろうなとは思ってはいるが……
しかし例えば n=2 のときの等式 "(1/1-1/3)+(1/2-1/4)=(1/1+1/2)-(1/3-1/4)" は一般の
"(1/1-1/3)+…+(1/n-1/(n+2))=(1/1+1/2)-(1/(n+1)+1/(n+2))"
に n=2 を代入したものと (特に右辺の形までくれば項の数まで過不足なく) まったく一致するので, n=1,2 がともに疑問だということになぜなのだろうかと足踏みしていました.
n=1 のときは「たまたま一致する」という認識でもいいのではと回答しようと思っていたからです.
# ただもちろん, n=1 のときは, 等式に代入する時点で右辺は 1/2 と -1/(n+1) が同じ項 (だから打ち消し) で
# "(1/1+1/2)-(1/(n+1)+1/(n+2))=1/1-1/3" になるので,
# また左辺 (1/1-1/3)+…+(1/n-1/(n+2)) のほうは項がたくさんあるように見えて
# 1/n-1/(n+2) =1/1-1/3 の一つがあるだけなので, 一致するのは必然なのだけれど,
# これを例えば通分して (n(3n+5))/(2(n+1)(n+2)) のような閉じた式でかいてあると
# 「式の内部で足し引き打ち消し合ってる」というような感覚は持ちづらいのもわかるという意図です.
## まあ部分和の話で "n=1 だけ例外" みたいなのはよく見かけるものではありますし.
"…" とか Σ とかでは, こういう「別のところにあるように見えて実は実体が同じ」とか, 「見かけ上あるように見えて実は存在しない虚像」とかそういう "記号の妙" があるので, そのへんは場合によっては好みの問題などで済ませるところではないか, という話を想定していたというところです.
|
No.87939 - 2024/04/26(Fri) 14:12:03 |
|