いつもお世話になっております。
解説でわからないところがあるので教えて欲しいです。
次の問題の解答で、⑵以降の先の考え方がわかりません。説明をよろしくお願いいたします。
![]() |
No.40510 - 2016/11/25(Fri) 10:26:28
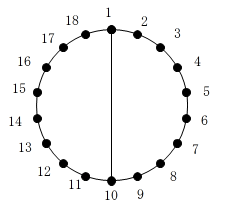
| ☆ Re: 場合の数 / ヨッシー  | | | 例えば、n=3(18角形)とします。
(2)
1つの直径 1-10 を決めると、それ以外の16個(6n-2個)の頂点とで、出来る三角形
1-10-2, 1-10-3, 1-10-4, ・・・ 1-10-9, 1-10-11, ・・・1-10-18
は全て直角三角形です。
直径は全部で9本(3n本)選べるので、
9×16=144(個) (6n-2)・3n=18n^2−6n
(3)
頂点 1 を決めると、直線 1-10 に対して対称な2点(2と18, 3と17, ・・・ 9と11)を
選ぶと二等辺三角形が
1-2-18, 1-3-17, ・・・ 1-9-11
の8個出来ます。この内 1-7-13 は正三角形なので、除いておきます。
よって、頂点1個につき、正三角形でない二等辺三角形は7個(3n-2個)出来ます。
18×7=126 6n(3n-2)=18n^2−12n
これに正三角形 6個(2n個)を加え 132個 18n^2−10n個
(4)
1-3 と同じ長さの線は18本(6n本)引けます。
この直線と他の1点を結んで出来る鈍角三角形は1個(1-3-2)
1-4 と同じ長さの線は18本(6n本)引けます。
この直線と他の1点を結んで出来る鈍角三角形は2個(1-4-2, 1-4-3)
1-5 と同じ長さの線は18本(6n本)引けます。
この直線と他の1点を結んで出来る鈍角三角形は3個(1-5-2, 1-5-3, 1-5-4)
・・・
1-9(3n) と同じ長さの線は18本(6n本)引けます。
この直線と他の1点を結んで出来る鈍角三角形は7個(3n-2個)(1-9-2, 1-9-3, ・・・ 1-9-8)
よって、鈍角三角形の数は
18×(1+2+3+・・・+7)=18×28=504(個)
6n(3n-1)(3n-2)/2=27n^3−27n^2+6n
上に貼られた解答の考え方は、
頂点1を決めると、
2〜9 の 8個(3n-1個) から2個を選ぶか、
11〜18 の8個(3n-1個) から2個を選び、それと 1 との3点で三角形を作ると、
1 が鈍角でない鈍角三角形が出来ます。(1-2-3, 1-2-4, 1-2-5 など)
(以下略)
|
No.40516 - 2016/11/25(Fri) 23:21:04 |
|