この問題を自習して解けとのことなんですが、全く意味がわかりません。教科書を見ながらやっているのですが、わかりません。
どのような図形をしているのか調べよ。というところで、どのような式が出てきて、どう答えればいいのか教えてください。
下に書いたある式は無視してください。
![]() |
No.65629 - 2020/05/20(Wed) 11:44:03
| ☆ Re: / ヨッシー  | | | そうすると、図に書き込んである通り、
3x+4y+5z=2
が表す平面となります。
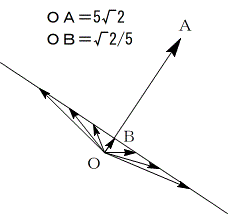
どのような図形かと言うと、これも書かれている通り、
(2/3,0,0) を通ってaに垂直な平面
でも良いですが、そもそも、内積値が一定ということはどういうことかと言うと、
ベクトルx のaへの射影が常にOBになるということです。
Bは、OA×OB=2となる点で、
B(3/25, 4/25, 1/5)
この点を通り、aに垂直な平面がVが表す平面です。
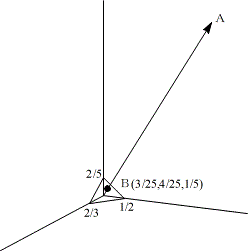
空間座標内の図は、上のようになります。
x軸、y軸、z軸との切片は (2/3,0,0), (0,1/2,0), (0,0,2/5)
で、この3点を通る平面で、aに垂直です。
|
No.65656 - 2020/05/20(Wed) 22:31:20 |
| ☆ Re: / 新大学生 | | | > そうすると、図に書き込んである通り、
> 3x+4y+5z=2
> が表す平面となります。
>
> どのような図形かと言うと、これも書かれている通り、
> (2/3,0,0) を通ってaに垂直な平面
> でも良いですが、そもそも、内積値が一定ということはどういうことかと言うと、
> ベクトルx のaへの射影が常にOBになるということです。
> Bは、OA×OB=2となる点で、
> B(3/25, 4/25, 1/5)
> この点を通り、aに垂直な平面がVが表す平面です。
>
>
> 空間座標内の図は、上のようになります。
> x軸、y軸、z軸との切片は (2/3,0,0), (0,1/2,0), (0,0,2/5)
> で、この3点を通る平面で、aに垂直です。
ありがとうございました。
|
No.65663 - 2020/05/21(Thu) 08:29:26 |
|