(1)はベクトルを使って表せましたが、(2)から全く歯がたちません。できれば、(1)から(2)まで詳しい解説をしていただけないでしょうか?
![]() |
No.73038 - 2021/02/22(Mon) 13:27:04
| ☆ Re: 数lll / ヨッシー  | | | (1)
αの式は
x+y+z−a=0
です。ここで、
f(x,y,z)=x+y+z−a
とおきます。
線分ABと共有点を持つためには、
f(1,0,0)<0 かつ f(1,2,0)>0
線分EFと共有点を持つためには、
f(1,0,1)<0 かつ f(1,2,1)>0
これらより、
1−a<0 かつ 3−a>0 かつ 2−a<0 かつ 4−a>0
以上より
2<a<3
(2)
a=5/2 は、(1) の範囲にあるので、AB、EFと交わり、
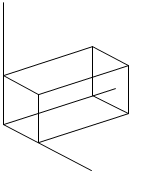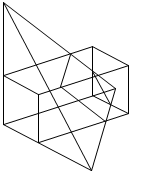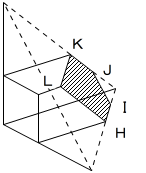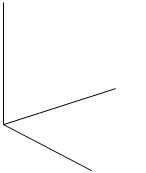
結果として、断面は図のような五角形になります。
これを、図のように、H,I,J,K,Lとすると、各座標は
H:x+y+z=5/2 にx=1,z=0 を代入して (1, 3/2, 0)
以下同様に
I:(1/2, 2, 0)
J:(0, 2, 1/2)
K:(0, 3/2, 1)
L:(1, 1/2, 1)
となります。これを、z軸回りに回すと、このようになります。
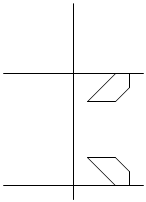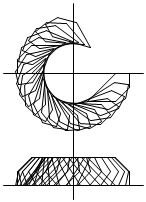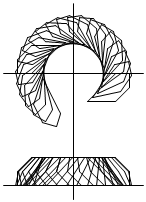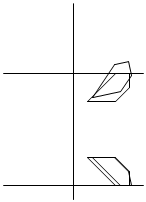
z軸に垂直な面で回転体を切ったとき、HIあるいはLKに平行な線分が
回転したときのドーナツ型になります。
線分LH上で、x=y となるのは、中点(1, 1, 1/2) です。
よって、
z座標が 1/2 以下の位置では、線分IJ上の点がz軸から一番遠く、
線分LH上の点がz軸から一番近くなります。
一方、z座標が 1/2 以上の位置では、線分JK上の点がz軸から一番遠く、
x=y となる点がz軸から一番近くなります。
z座標zの位置で五角形HIJKLを切ったときを考えます。
0≦z≦1/2 において、
IJ上の点は (1/2-z, 2, z) z軸から遠い
LH上の点は (1, 3/2-z, z) z軸に近い
断面積は
π{(1/2-z)^2+2^2−1^1−(3/2-z)^2}
=π(2z+1)
1/2≦z≦1
JK上の点は (0,5/2-z, z) z軸から遠い
x=y の点は (5/4-z/2, 5/4-z/2, z) z軸に近い
断面積は
π{(5/2-z)^2−(5/4-z/2)^2−(5/4-z/2)^2}
=π(z^2/2−5z/2+25/8)
それぞれ積分して
π∫[0〜1/2](2z+1)dz+π∫[1/2〜1](z^2/2−5z/2+25/8)dz
=(73/48)π
検算してください。
|
No.73042 - 2021/02/22(Mon) 18:52:01 |
|