この問題そもそも問題が何を説明しているのかわかりません。図示して説明していただけると助かります。そして、どうやって解いていくのか教えてほしいです。
![]() |
No.83484 - 2022/09/26(Mon) 01:37:38
| ☆ Re: ベクトル / ヨッシー  | | | 立体的な図では、余計わからなくなるので、
平面αが直線に見える方向から見た図を描きます。
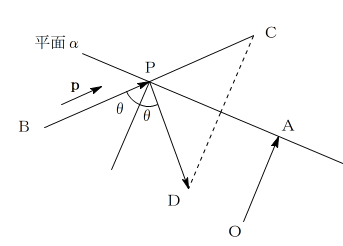
(1)
点A(1,2,-1) を通り、ベクトル(1,2,-1) に垂直な平面の式は
(x-1)+2(y-2)−(z+1)=0
x+2y−z=6 ・・・α
点B(-3,-2,-1) を通り、ベクトル(1,1,1) に平行な直線の式は、
tを実数として、
x=t−3、y=t−2、z=t−1 ・・・(i)
と書けます。これと、αとの交点Pを求めるために、αの式に代入して、
(t-3)+2(t-2)−(t-1)=6
2t=12
t=6
これを(i)に代入すると、点Pの座標は
P (3,4,5) ・・・答え
(2)
図において、BPの方向に点Cを取り、点Cと平面αに関して
対称な点をDとすると、PDの方向が求めるベクトルの方向となります。
ここでは、計算しやすいように、BP=CPとします。
点Cの座標は
2(3,4,5)−(-3,-2,-1)=(9, 10, 11)
Cを通り平面αに垂直な直線の式は
x=t+9、y=2t+10、z=−t+11
αの式に代入して、
(t+9)+2(2t+10)−(-t+11)=6
6t=−12
t=−2
よって、CDの中点(α上の点)の座標は
(7, 6, 13)
よって、点Dの座標は
2(7, 6, 13)−(9, 10, 11)=(5, 2, 15)
ベクトル
PD=(2, -2, 10)
の大きさは
√(4+4+100)=6√3
よって求める単位ベクトルは
±(1/3√3, −1/3√3, 5/3√3)・・・答え
|
No.83486 - 2022/09/26(Mon) 11:28:18 |
|