xyz空間内の1辺の長さ1の立方体OABC-DEFGについて考える。
Oを原点、Fを(√3,0,0)におく。このとき、残りの頂点について、B、Dをxy平面上に来るようにおくとき、残りの頂点を求めなさい。ただしDのy座標は正とする。
B(2/√3,-√2/√3,0)、D(1/√3,√2/√3,0)の2点は何とか求められましたが、ここから先がさっぱり分からないです。図のイメージも湧かないです。
どうやればよいのでしょうか。教えてください。お願いします。
|
No.10024 - 2010/03/20(Sat) 22:01:50
| ☆ Re: 立方体の頂点 / ヨッシー  | | | BとDがわかっているので、
Bをx軸周りに120°回転した点がG、-120°回転した点がE。
Dをx軸周りに120°回転した点がA、-120°回転した点がC。
となります。
|
No.10025 - 2010/03/21(Sun) 00:55:44 |
| ☆ Re: 立方体の頂点 / rtz | | | OBDFがxy平面上にあるから、
面OABCや面DEFGはxy平面と垂直に交わる。
このことから、
A,Cからxy平面上におろした垂線の足は、OBの中点と一致する。
E,Gも同様。
|
No.10026 - 2010/03/21(Sun) 00:57:41 |
| ☆ Re: 立方体の頂点 / 西田 | | | 早速の御回答ありがとうございます。
ヨッシー様のごヒントを参照に残りの座標を計算したら、
A(√2/2√3,-√2/2,0)
C(√2/2√3,√2/2,0)
G(-√2/2√3,√2/2,0)
E(-√2/2√3,-√2/2,0)
となりましたが、この結果はあっていますでしょうか。
それと再度質問ですが、
『Bをx軸周りに120°回転した点がG、-120°回転した点がE。
Dをx軸周りに120°回転した点がA、-120°回転した点がC。』
こうなる理由が分からないです。どうやって見つけられたのでしょうか。その過程をもう少し教えていただけないでしょうか。お願いします。
rtz様
『面OABCや面DEFGはxy平面と垂直に交わる。』
これは間違っていませんでしょうか。自分の図が間違っているのかもしれませんが…
|
No.10027 - 2010/03/21(Sun) 01:43:48 |
| ☆ Re: 立方体の頂点 / rtz | | | あ、ホントですね。
思いっきり考え違いをしていました。
申し訳ありません、私の分は忘れてください。
|
No.10028 - 2010/03/21(Sun) 04:22:51 |
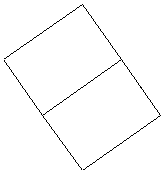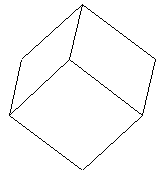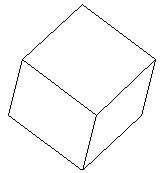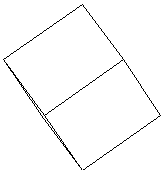
| ☆ Re: 立方体の頂点 / ヨッシー  | | | 上に貼り付けた図の、上の方向(点Oと点Fが重なる方向)から見ると、
点Fから辺FB、辺FE、辺FGがそれぞれ、均等な方向に伸びています。
よって、対角線OF(x軸)を中心に120°ずつの関係になります。
どちらが120°で、どちらが-120°かは、図を描いて判断するのが
良いでしょう。
|
No.10029 - 2010/03/21(Sun) 05:20:54 |
|