3点O(0、0)、A(1、0)、B(0、1)、C(1、1)に対して、点P(α、β)が次の図形の周と内部を動くとき点Q(α+β、αβ)の動く範囲をそれぞれ図示せよ。
(1)三角形OAB(2)四角形OACB
教えて下さい、お願いします
(高校 2 年)
|
No.7033 - 2009/07/30(Thu) 19:29:35
| ☆ Re: また質問があります / ヨッシー  | | | 線分OA上の点の座標は、(t,0) (0≦t≦1) と書けるので、Qの座標は、(t,0)
線分OB上の点の座標は、(0,t) (0≦t≦1) と書けるので、Qの座標は、(t,0)
線分AB上の点の座標は、(t,1-t) (0≦t≦1) と書けるので、Qの座標は、(1,t-t^2)
さらに、
線分AC上の点の座標は、(1,t) (0≦t≦1) と書けるので、Qの座標は、(t+1,t)
線分BC上の点の座標は、(t,1) (0≦t≦1) と書けるので、Qの座標は、(t+1,t)
以上より、点Pが
線分OA上を動くとき、点Qは線分OA上を動く。
線分OB上を動くとき、点Qは線分OA上を動く。
線分AB上を動くとき、点Qは線分AD上を動く。ただし、D(1,1/4)
線分AC上を動くとき、点Qは線分AE上を動く。ただし、E(2,1)
線分BC上を動くとき、点Qは線分AE上を動く。ただし、E(2,1)
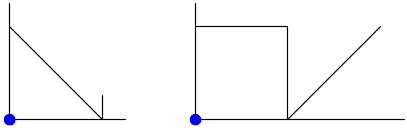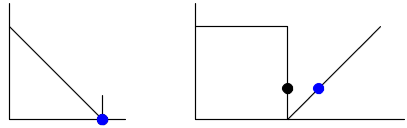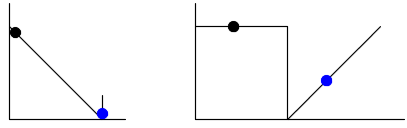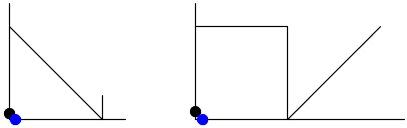
|
No.7034 - 2009/07/30(Thu) 20:25:31 |
| ☆ Re: また質問があります / rokku | | | すみません。点Eというのは自分で置くのでしょうか?
|
No.7035 - 2009/07/30(Thu) 20:42:51 |
| ☆ Re: また質問があります / ヨッシー  | | | 点Dもおきますよ。
別に、DとかEは設定しなくても良いのですが、
点Aと点(1,1/4) を結んだ線分上を動く。よりは、
線分AD上を動く。とした方が、表現がそろうので、
そうしただけです。
|
No.7038 - 2009/07/30(Thu) 21:31:17 |
| ☆ Re: また質問があります / rokku | | | No.7040 - 2009/07/30(Thu) 21:33:27 |
| ☆ Re: また質問があります / angel | | | 横から失礼します。
「次の図形の周と **内部** を動くとき」とありますから、答は直線/曲線ではなく、直線/曲線で囲まれた領域になると思うのですが…?
|
No.7045 - 2009/07/31(Fri) 00:14:44 |
| ☆ Re: また質問があります / ヨッシー  | | | あ、そうですね。
では、やり直し(^^;
(1)△OABの周および内部の点の座標は、
(s,t) (0≦s, 0≦t, s+t≦1)
と書けるので、Qの座標は
(s+t, st)
x=s+t, y=st と置くと、相加相乗平均より
√st≦(s+t)/2
√y≦x/2
y≦x^2/4
図の添付が1個しか出来ないので、(2) は↓次。
![]() |
No.7046 - 2009/07/31(Fri) 08:31:46 |
| ☆ Re: また質問があります / ヨッシー  | | | (2)
四角形OACBの内部の点の座標は、
(s,t) (0≦s≦1, 0≦t≦1)
と書けるので、Qの座標(s+t, st)は、
y座標の最大値は、同じく y≦x^2/4 ですが、
最小値は、0≦x≦1 では、y=0
1≦x≦2 では、上記の y=x−1となります。
![]() |
No.7047 - 2009/07/31(Fri) 09:07:49 |
|
