[ 掲示板に戻る ]
過去ログ閲覧モード
★ 対数 / 鴇
初めまして！
対数の問題が分からないので
教えて頂けたら嬉しいです！

0.8^nがはじめて0.1より小さくなるような
正の整数nの値を求めよ。


色々な参考書を見ましたが
分かりませんでした……
宜しくお願いします！
No.6093 - 2009/06/02(Tue) 00:50:05
☆ Re: 対数 / 雀
0.8^n＜0.1
常用対数をとれば
n(log8-log10)<-1
n>-1/(log8-log10)=-1/(3log2-1)=10.3188･･･
よって
n=11
No.6095 - 2009/06/02(Tue) 06:27:13
☆ Re: 対数 / 鴇
なるほど！
まずは不等式を作ればいいんですね！

ありがとうございます
No.6106 - 2009/06/02(Tue) 21:06:29
★ 数学的帰納法 / 高二の父
よろしくお願いします。
問題
1ｇ，2ｇ，4ｇ・・・，(2^n-1)ｇの分銅が各1個あれば、これらを組み合わせて１ｇから(2^n-1)ｇまでの1ｇごとの重さが作られることを証明したいのですが。
No.6092 - 2009/06/02(Tue) 00:23:07
☆ Re: 数学的帰納法 / ヨッシー
分銅の方は、2^(n-1) で、量れる重さの方は (2^n)-1 ですね。

数学的帰納法とタイトルにあるので、それでやってみます。
n=1 のとき、１ｇの分銅1個で、１ｇまでの重さは量れます。
n=k のとき、1,2,・・・2^(k-1)ｇ の分銅1個ずつあれば、
1gから(2^k)-1g の重さが量れるとき、
n=k+1 について考えます。
つまり、2^kｇの分銅が1個加わったとすると、
今まで量れていた、1gから(2^k)-1g の次の重さ、2^k g は、
加えた分銅1個で量ることができ、その次からは、2^k g の
分銅に、それ以外の分銅で作れる、1gから(2^k)-1g を加えることにより
(2^k)+1, (2^k)+2, ・・・, (2^k)+(2^k)-1
までが、１ｇ刻みで量れます。
　(2^k)+(2^k)-1＝2^(k+1)-1
であるので、n=k+1 についても、1gから(2^n)-1g までが
量れることがいえます。

以上より、任意の自然数ｎについて、題意を満たします。

なお、一般には、２進数を使って説明することが多いですね。
No.6096 - 2009/06/02(Tue) 06:50:58
☆ Re: 数学的帰納法 / 高二の父
問題を書き間違えたにも関わらず、解答いただきありがとうございました。
No.6098 - 2009/06/02(Tue) 09:05:50
★ 微分 / さち
はじめまして。
座標平面上を運動する点Pの、時刻tにおける座標（x,y）が
x=2cost-cos2t、y=2sint-sin2t
で表されるとき、Pの速さの最大値を求めよ。
ただし、0≦t≦2πとする。

という高３の問題なんですが、どうしても解けないんです。
解き方を教えてください。お願いします。
No.6090 - 2009/06/01(Mon) 22:00:42
☆ Re: 微分 / ヨッシー
速さの公式
Ｖ＝√{(dx/dt)2+(dy/dt)2}
に代入すると、
Ｖ＝√(8-8cost)
になります。ｔ＝π のとき最大値４となります。
No.6097 - 2009/06/02(Tue) 08:15:06
★ 関数 / champagne
aが定数のとき、f(θ)=a((√3)sinθ-cosθ)-((√3)sin2θ+cos2θ)+a+1 , 0≦θ≦πとする。
方程式f(θ)=0が相異なる３つの実数解をもつようなaの値の範囲を求めよ。という問題です。

とりあえず、(√3)sinθ-cosθ=2sin(θ-π/6)に合成し、t=(√3)sinθ-cosθとして、f(θ)=t^2+at+a-1というtの２次関数に帰着させました。

-1≦t≦2はでましたがその先がつまってしまったので、どうか教えてください。
No.6084 - 2009/06/01(Mon) 17:22:55
☆ Re: 関数 / ヨッシー
　f(θ)=t^2+at+a-1=(t+1)(t+a-1)
であるので、f(θ)＝０ の解は、ｔ＝-1, 1-a です。
　t=(√3)sinθ-cosθ=2sin(θ-π/6)
より、t=-1 を満たすのは、0≦θ≦π の範囲では θ＝０ の１つだけです。
ですから、ｔ＝1-a より、θの解が２つ出来ればいいことになります。
0≦θ≦π の範囲で、2sin(θ-π/6) が２つのθについて、同じ値を
取るのは、　1/2≦sin(θ-π/6)＜1 のときであるので、
各辺２倍して
　1≦ｔ＜2
代入して
　1≦１−ａ＜２
変形して
　-1＜ａ≦0
となります。
No.6085 - 2009/06/01(Mon) 17:45:10
☆ Re: 関数 / champagne
なるほど！
因数分解を疑うのを忘れていました。
ありがとうございました！
No.6086 - 2009/06/01(Mon) 19:35:41
★ 極限 / aki
こんにちは(^^)
どうか質問お願いします！
Σ[K=1〜n]cos2Kπ/3の解き方、考え方を教えて下さい(>_<)
具体的に代入して考えてみると、cos2/3=−1/6、cos4/3=−1/6なのでいまいち統一性がなく、よくわからないなと困ってしまいました(>_<)
n=3M−2 3M−1 3M
で場合わけするようですがそれもよくわかりません、
どうか教えて下さい…
No.6080 - 2009/06/01(Mon) 15:30:31
☆ Re: 極限 / ヨッシー
ちょっと、集中力が、散漫になってますね。
＞cos2π/3=−1/2、cos4π/3=−1/2
ですね。数列で書くと
　-1/2, -1/2, 1, -1/2, -1/2, 1, ・・・
の繰り返しです。和で言うと、
　-1/2, -1, 0, -1/2, -1, 0, ・・・
です。n=3M−2, 3M−1, 3M で場合わけの理由が、わかると思います。
No.6081 - 2009/06/01(Mon) 15:50:39
☆ Re: 極限 / aki
しばらく三角関数に触れて無かったのでまったく勘違いをしておりました(>_<)ごめんなさい(>_<)
数列だけではなく和も考えていくと和も繰り返しになっているのですね！わかりましたありがとうございます!
No.6126 - 2009/06/03(Wed) 15:41:45
★ 三角関数 / 高二の父
先日は、皆さんから助けをいただきありがとうございました。
今日は、三角関数です、実は物理の問題を解いていて、困ったことが・・・。
ｓｉｎθ・ｃｏｓθが最大となるのは、θ＝４５度のときの０．５と思うのですが、証明ができません。
私の、予想の答えの正否も含め教えてください。
No.6078 - 2009/06/01(Mon) 11:13:56
☆ Re: 三角関数 / ヨッシー
倍角の公式
　sin(2θ)＝2sinθcosθ
を使うと、
　sinθcosθ＝(1/2)sin(2θ)
となり、最大値は、2θ＝90°, θ＝45° などのときで、
最大値は 1/2 です。
「など」と書いたのは、
　θ＝45°, 225°, 405° など色々あるからです。
一般的には、0°≦θ＜360° で見るので、この場合は、
　θ＝45°, 225°のとき、最大値は 1/2 となります。
No.6079 - 2009/06/01(Mon) 11:22:30
☆ Re: 三角関数 / 高二の父
> 倍角の公式
> 　sin(2θ)＝2sinθcosθ
> を使うと、
> 　sinθcosθ＝(1/2)sin(2θ)
> となり、最大値は、2θ＝90°, θ＝45° などのときで、
> 最大値は 1/2 です。
> 「など」と書いたのは、
> 　θ＝45°, 225°, 405° など色々あるからです。
> 一般的には、0°≦θ＜360° で見るので、この場合は、
> 　θ＝45°, 225°のとき、最大値は 1/2 となります。

わかりました！
ありがとうございました。
No.6087 - 2009/06/01(Mon) 20:43:32
★ (No Subject) / むささび３年
指数の問題です。

(１)　81^3/4


(２) 64^2/3

この２つの問題は法則にあてはめて地道に解いていくしかないのですか？

工夫すればなにか簡単な解法があると思うのですが・・・
よろしくおねがいします。
No.6069 - 2009/05/31(Sun) 19:03:06
☆ Re: / ヨッシー
法則とは、公式
　（ａm)n＝ａmn
のことでしょうか？

上のような問題では、この公式に入れて解くのが、最も簡単
かつ確実な方法だと思います。

64＝43 がすぐに思いつけば、多少は楽ですが、
そういう人は、普通に、上の公式に当てはめても、苦もなく
解けるものです。
No.6071 - 2009/05/31(Sun) 20:43:08
☆ 横から失礼 / BossF
楽な方法というより定石（←読める？）なんですが

底を素因数分解します

例えば81^3/4=(2^4)^3/4=2^3

なんですが、ヨッシーさんが言われてるのは、「こんなのは九九みたいなもんですぐ慣れますから解き方で悩む暇があったら計算しましょう！！」ちゅうことだと思います、←私も同感です
No.6076 - 2009/06/01(Mon) 00:59:27
★ 2次不等式 / ぬっち

2次不等式kx^2-2(k+1)x+4k+2>0が解をもたないようなkの値の範囲を求めよという問題なのですが、いまいち解き方が分からないので分かる方ご指導宜しくお願いします。


No.6068 - 2009/05/31(Sun) 18:37:04
☆ Re: 2次不等式 / ヨッシー
(2次式)＞０の形の不等式が解を持たないのは、
ｙ＝(2次式) のグラフが、下に凸　かつ　判別式＜0　です。

一方、(2次式)＜０の形の不等式が解を持たないのは、
ｙ＝(2次式) のグラフが、上に凸　かつ　判別式＜0　です。
No.6072 - 2009/05/31(Sun) 20:45:14
★ 格子点 / aki
いつもお世話になっております！
質問お願い致します(>_<)
http://v.upup.be/?lWNLcrSkTI
の(1)で図を書くと三つの領域に分かれるのですが、全体から白い二つをひくという方法をとって、二つは同じなので下の領域について取り出して考えてみて、
http://u.upup.be/?mlRUJoYJXC
なのでY=K=0の時を別に考え、 格子点の数は
31＋Σ[K=1〜30](30−3k)
を2倍と考えたのですが答えが合いません。どうしてでしょうか？（？＿？）
どなたかお願いします(>_<)
No.6067 - 2009/05/31(Sun) 16:50:23
☆ Re: 格子点 / ヨッシー
全体とか、白い二つとか、はっきりとは書かれていませんが、
たぶん、こういうことでしょう。


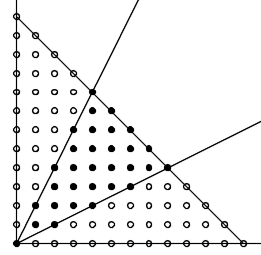
それを踏まえて、お答えすると、
ｙ＝ｋ＝０　を、特別扱いする必要はありません。
足す範囲は、ｋ＝１〜30ではありません。
もちろん、ｋ＝０〜30でもありません。

これを元に、もう一度考えてみてください。
No.6070 - 2009/05/31(Sun) 20:38:19
☆ Re: 格子点 / angel
蛇足かも知れませんが。
問題は S[30] つまり、n=30の時の値を求めるようになっていますが、実際にこの状況だと、規模が大きくて、手で数えるのには無理があります。つまり、これは、「一般項を求めよ」と言われているのと同じことだと思ってください。
※いっそのこと、一般項を求めてから、n=30 の値を当てはめて計算しても良いくらいです。

で、一般項を求めるのには何をすれば良いか。それは、「規則性を正確に掴む」ことです。上でヨッシーさんが挙げられているように、nが小さい時の状況(上ではn=12)を描いてみることが基本です。(自信がなければ、1例だけでなく2,3例描いて数えてみる)

後、先に(2)の問題に着目してください。(どんな問題でも、先の方の小問を解く前に、必ず後の小問の内容をチェックしましょう)
S[3n] という形が出てきているかと思います。
これを元に考えると、(1)のS[30]というのは、S[1],S[2],…,S[30]という30番目(もしくは、S[0]から数えて31番目)とは考えてはいけない、ということが分かります。
そうではなく、S[3],S[6],…,S[30]という10番目(もしくは、S[0]から数えて11番目)と考える問題なのです。
このことを把握していれば、上のヨッシーさんの回答にある「k=1〜30ではありません」の意味がわかると思います。
No.6075 - 2009/05/31(Sun) 22:39:44
☆ Re: 格子点 / angel
別解として
　S[30]=1+(0+1+2)+(1+2+3)+(2+3+4)+…+(9+10+11)
　※()の数は10組、足しこんでいる項の数は31
というのもあります。
x+y≦n ( n=30 ) を、x+y=0 or x+y=1 or … or x+y=3k-2 or x+y=3k-1 or x+y=3k or … or x+y=30 と分解して考えた場合、このような計算になります．
No.6083 - 2009/06/01(Mon) 16:27:56
★ 中学三年生です / くねちゃん
8で割ると1余り、11で割ると10余る自然数のうち、5番目に小さいものを求めなさい。

という問題なのですが解き方がわかりません・・・

ご回答よろしくお願いします。
No.6058 - 2009/05/31(Sun) 00:11:09
☆ Re: 中学三年生です / らすかる
「8で割ると1余り、11で割ると10余る自然数」に7を足すと
「8で割リ切れ、11で割ると6余る自然数」になります。
これに8を足すと「8で割リ切れ、11で割ると3余る自然数」
さらに8を足すと「8で割リ切れ、11で割リ切れる自然数」
となり、結局元の自然数に23を足すと88で割り切れますので、
条件を満たす自然数は88の倍数から23を引いたものです。
No.6059 - 2009/05/31(Sun) 00:56:59
☆ Re: 中学三年生です / roro
参考の一例(概略)です。

8で割ると1余る自然数
…{1，9，17，25…}
●自然数xを用いて、(8x−7)と表すことができます。

11で割ると10余る自然数
…{10，21，
●自然数yを用いて、(11y−1)と表すことができます。

8x−7＝11y−1　から
　8x＝11y＋6
　　(両辺に16を加えます)
　8x＋16＝11y＋22
　8(x＋2)＝11(y＋2)
　(x＋2)：(y＋2)＝11：8

自然数kを用いて、
　(x＋2)＝11k，(y＋2)＝8k　と表すことができることから
　　x＝11k−2，y＝8k−2

求める数の条件【8x−7＝11y−1】から
　8{11k−2}−7＝11{8k−2}−1＝88k−23　と表されて

k＝1，2，3，4、5，6，…　から
　65，153，241，329，417，505，…

よって、求める数は、417
No.6060 - 2009/05/31(Sun) 01:02:04
☆ Re: 中学三年生です / roro
＞らすかるさん　
　　すみません。　かぶってしまいました。

＞くねちゃん さん　
　　らすかるさんの簡潔な表現を参考にしてください。
No.6061 - 2009/05/31(Sun) 01:05:55
☆ Re: 中学三年生です / くねちゃん
らすかるさん、roroさん

ご丁寧な回答ありがとうございました。

理解できました。

また質問がある時はお世話になりたいと思います。
No.6062 - 2009/05/31(Sun) 01:09:37
★ sinθ、cosθで表された関数 / 山岸

関数y=cos^2x＋sinx(0≦x≦π)の最大値、最小値およびそのときのxの値を求めよ。
という問題なのですが、数?Tでの解き方も数?Vでの解き方もあるそうなのですが、どなたか分かる方両方ともよろしくお願いします。
No.6052 - 2009/05/30(Sat) 20:49:08
☆ Re: sinθ、cosθで表された関数 / angel
数I
　t=sinx とおくと、tの範囲は 0≦t≦1 であり、
　y=(cosx)^2+sinx=1-(sinx)^2+sinx=-t^2+t+1 です。
　ここから、t=1/2の時y最大、t=0,1の時y最小と分かります

数III
　dy/dx=-2sinx・cosx+cosx=-2cosx・(sinx-1/2) となることから、yの増減を調べると、
　x=0→増加→sinx=1/2で極大→減少→cosx=0で極小→増加→sinx=1/2で極大→減少→x=π
　という推移になります。
No.6054 - 2009/05/30(Sat) 21:16:19
☆ Re: sinθ、cosθで表された関数 / ハオ
僕はまだ数?VCを未履修なので数?Tの解き方を記したいと思います。
y=cos^2x+sinx
=(1-sin^2x)+sinx
=-sin^2x+sinx+1
=-(sinx-1/2)^2 +5/4
0≦x≦πより0≦sinx≦1
この範囲でグラフを書けば
Max:5/4 (x=π/6)
min:1 (x=0, π)
No.6055 - 2009/05/30(Sat) 21:17:29
★ 一つの円での弦と弧と円周角 / たけし
?@ある円上の点Ａ、Ｂ、Ｃ、Ｄにおいて
弧ＡＢの長さと弧ＣＤの長さが等しいならば、
弦ＡＢの長さと弦ＣＤの長さは等しい。

これは真ですよね？

?Aある円上の点Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆにおいて、
∠ＡＢＣ＝∠ＤＥＦならば、
弧ＡＣの長さと弧ＤＦの長さは等しい。

これも真ですよね？

よろしくお願いします。
No.6050 - 2009/05/30(Sat) 19:58:35
☆ Re: 一つの円での弦と弧と円周角 / ヨッシー
両方真です。
△ＡＢＯと△ＣＤＯ、△ＡＣＯと△ＤＦＯ　が
それぞれ、２辺挟角相等で合同なため。
No.6051 - 2009/05/30(Sat) 20:48:01
☆ Re: 一つの円での弦と弧と円周角 / たけし
ありがとうございます。当たり前のように使ってたのですが少し気になってしまいまして。
No.6063 - 2009/05/31(Sun) 06:56:40
★ ベクトル / マルス
正三角形ABCを辺AB、BC、CAを軸にして折り返すことを繰り返して、平面上にたくさんの正三角形を作る。
このとき、AP→=2005AB→+2AC→を満たす点Pは正三角形の頂点A、B、Cのどれかに到着する。どの頂点に到着するか。
また線分APは三角形ABCの辺と何回交わるか。

実力テストの問題だったんですが、解き方がまるでわかりませんでした。どうやって解くのかわかりやすく教えてもらえないでしょうか？よろしくお願いします。
No.6046 - 2009/05/30(Sat) 18:26:19
☆ Re: ベクトル / ヨッシー

どちらの方向に折り返しても、点Ａ，Ｂ，Ｃは、
図のような位置に来ます。

図の太線が、最初の三角形とすると、
ＡＰ＝2005ＡＢ＋2ＡＣ
となる点Ｐは、図の、右下向きの矢印の先の点Ｂから、
左下にＣ，Ａ，Ｂ，Ｃ，Ａ，Ｂ，・・・
と2005個分進みます。2005は3で割って、１余る数なので、
点Ｐは、Ｃになります。


たとえば、
ＡＰ＝3ＡＢ＋2ＡＣ
で考えます。
ＡＢ方向に３進んでおり、その間にＡＣ方向の直線を
２回（＝３−１）横切ります。
ＡＣ方向に２進んでおり、その間にＡＢ方向の直線を
１回（＝２−１）横切ります。
ＢＣ方向の直線は４回（３＋２−１）横切ります。
３と２は互いに素なので、合計７回辺と交わります。

2005と2の場合は、
　2004＋１＋2006＝4011(回)
となります。
No.6056 - 2009/05/30(Sat) 21:24:39
☆ Re: ベクトル / マルス
ヨッシー様！図を添えてお答えしていただけるとは思いませんでした。ありがとうございます。

＞2005個分進みます。2005は3で割って、１余る数なので、
点Ｐは、Ｃになります。

これはAB→の係数が1ならBに、2ならCに、3ならAに、4ならBに、・・・と周期3でB→C→Aと変化するということですよね？なるほど…。

＞2004＋１＋2006＝4011(回)

すみません、ここのところ考えてみたんですがどうしてこういう計算になるのかどうしてもわからないです。もう少し詳しく教えてもらえないでしょうか？お願いします。
No.6065 - 2009/05/31(Sun) 15:15:17
☆ Re: ベクトル / ヨッシー

図は、ＡＰ＝９ＡＢ＋２ＡＣ の例です。
９ＡＢ から、赤い線が　８本あることがわかります。
２ＡＣ から、青い線が　１本あることがわかります。
緑の線は、赤い線に対して１本ずつ、青い線に対して１本ずつと、
もう１本（右上の角)あるので、８＋１＋１＝１０(本)あります。
ＡＰ は、それらをすべて１回ずつ横切るので、
８＋１＋１０＝１９(個)の交点が出来ます。
（No.6056 の記事では、９＋２−１ としていますが、同じことです。）

これを、ＡＰ＝2005ＡＢ＋2ＡＣ に当てはめると、
それぞれ、2004, 1, 2006 になります。
No.6077 - 2009/06/01(Mon) 09:37:48
☆ Re: ベクトル / マルス
ヨッシー様！今度は納得できました。ありがとうございました♪

…本当に納得できたのか文字で試してみたのですが、AP→=mAB→+nAC→の場合なら、青い線とn-1回、赤い線とm-1回、緑の線と(m-1)+(n-1)+1回交わる、となると思いますが、よろしければこちらで正しいかどうか教えていただけないでしょうか。
No.6091 - 2009/06/01(Mon) 23:11:37
☆ Re: ベクトル / ヨッシー
それで良いですね。

数え方によっては、緑はｍ＋ｎ−１と理解する人も
いるかもしれません。つまり、
点Ａから点Ｐまで、外周に沿っていく道が、ｍ＋ｎ本の辺が
あるうちの、辺と辺の間に緑の線があるので、
という考え方です。
No.6099 - 2009/06/02(Tue) 11:45:50
☆ Re: ベクトル / マルス
最後までご丁寧にありがとうございました。完全に解決しました！
No.6109 - 2009/06/02(Tue) 22:13:14
★ 極限 / aki
こんばんは。
度々お世話になります。
前にも似たようなことを質問したのですがわけが分からなくなってしまいましたので新たに再質問させてください。
http://v.upup.be/?j7mYB0JkcT
の(3)なのですが、x^n{f(x)−1/2x^2}を
http://u.upup.be/?hH1jzHmLcZまで変形できました
分母が2に収束するので分母の収束条件はx^nが収束することでn<0かn=0かなと思ったのですが、そうすると正答とは異なるみたいです。
どこが間違いでしょうか？
No.6044 - 2009/05/30(Sat) 18:02:42
☆ Re: 極限 / angel
前の質問の所に、少しコメントを載せました。参考にしてみて下さい。
No.6049 - 2009/05/30(Sat) 19:19:22
☆ Re: 極限 / aki
こちらものせました…
二時間位考えてもわけがわからないので、困り果ててしまいました…
No.6089 - 2009/06/01(Mon) 21:46:19
★ 無限級数 / aki
こんにちは！
度々お世話になります。どうぞ宜しくお願いします(>_<)
http://r.upup.be/?d9lEKp9GkF
の(2)なのですが、(1)より予測してanは初項2/r^2 公比−1/r の等比数列2/r^2*(−1/r)^(n−2)とし、数学的帰納法で証明する
という方法で行ったのですが、一応証明もできたのですが答えが異なるようで、答えは2(−1)^n/r^n だそうです。
私のやり方では不可なのでしょうか？
どなたか教えて下さい。
No.6034 - 2009/05/30(Sat) 16:05:20
☆ Re: 無限級数 / だるまにおん
2/r^2*(−1/r)^(n−2) = 2(−1)^n/r^n です。
No.6040 - 2009/05/30(Sat) 17:08:51
☆ Re: 無限級数 / rtz
同じです。
2/r2 * (-1/r)n-2
＝2/r2 * 1 * (-1)n-2/rn-2
＝2 * (-1)2 * (-1)n-2/rn
＝2 * (-1)n/rn
(＝2 * (-1/r)n)

ただ、
rはまとめるべきですし、
nもできたら+1や-2などが付かない形の方が綺麗です。
今回のように、数列や極限、級数などの場合は、
式を上手くまとめられるようになっておいたほうがいいか思います。
No.6041 - 2009/05/30(Sat) 17:09:09
☆ Re: 無限級数 / rtz
＞だるまにおんさん
かぶってしまいました、申し訳ありません。
No.6042 - 2009/05/30(Sat) 17:09:46
☆ Re: 無限級数 / aki
ありがとうございます。
ちなみにこの(2)は数学的帰納法ではなく等比数列×等差数列の和と同じ方法でも解けるらしいのですが、anも等比数列 rも等比数列だからその方法では解けないと思うのですが、どうして解けるのでしょうか？
教えて下さい(>_<)
No.6045 - 2009/05/30(Sat) 18:10:45
☆ Re: 無限級数 / rtz
仰っていることがちょっと分かりませんが、
おそらく一番早いのは
n≧2
anrn
＝Σ[k＝1,n]akrk−Σ[k＝1,n-1]akrk
＝(-1)n−(-1)n-1
＝2(-1)n
⇔an＝2(-1/r)n
でしょう。
No.6048 - 2009/05/30(Sat) 19:13:10
☆ Re: 無限級数 / aki
はい、それは数列の分野でこういう変形の仕方は習うのでしょうか…?
情けないことに全く思い付かなかったのですが…
No.6064 - 2009/05/31(Sun) 15:00:03
☆ Re: 無限級数 / rtz
だいぶスレッドが下がってきましたが。

＞こういう変形の仕方
akiさんの学年は分かりませんが、数列の総和や級数など習う際に、
「第1項〜第n項の和をSnとすると、Sn＝2an−1である。anを求めよ。」
等の問題で、Sn−Sn-1＝an (或いはSn+1−Sn＝an+1)を扱うはずです。

今回はこれと同じことです。
No.6073 - 2009/05/31(Sun) 21:26:35
☆ Re: 無限級数 / aki
なるほど!ありがとうございます!全く思い付きませんでした…
典型問題じゃないとそれを使うとは思い付かないのですが、どう考えれば思い付くのでしょうか？

No.6082 - 2009/06/01(Mon) 15:56:27
★ 高校一年 / 麒麟
ax+2>x+3a^2-a
の解が
x<a^2-6a-20
であるときのaの値は？？

とても基本的な問題ですが
解き方が分かりません。
aの答えは-2です

宜しくお願いします
No.6033 - 2009/05/30(Sat) 14:52:15
☆ Re: 高校一年 / ヨッシー
ax+2>x+3a^2-a
をそのまま解くと
(a-1)x>3a^2-a-2
これの解が x<a^2-6a-20 となるには、
a-1＜０ で、両辺 a-1 で割って、
　ｘ＜(3a^2-a-2)/(a-1)＝3a+2
条件より、
　3a+2＝a^2-6a-20
整理して、
　a^2−9a−22＝０
これを解いて、
　a=11,-2
答えまで、もう一山ありますが、とりあえずここまで。
No.6037 - 2009/05/30(Sat) 16:33:20
☆ Re: 高校一年 / ハオ
こむばんわ。僕なりの解答を記しておきます。(勝手ながら)
ax+2>x+3a^2-aを整理して
x(a-1)>(a-1)(3a+2)
ここで重要なのが(a-1)が正負又は0の時で場合分けが必要です。何故なら不等号の向きが変わってしまうからです。
(i)a-1=0 即ちa=1の時
x×0>0⇔0>0となり不適。
(ii)a>1時
x>3a+2 題意より不適
(iii)a<1の時
x<3a+2
題意よりa^2-6a-20=3a+2となればよい。
これを解いてa=11,-2
故にa=-2(∵a<1)
No.6053 - 2009/05/30(Sat) 21:10:47
★ 確率 / りんご
何度も申し訳ないです。数直線上の原点に点Ｐがある。
さいころを投げて３か６の目が出れば正の向きに２、
それ以外の目が出れば負の向きに１だけ点Ｐを移動させる。
さいころを６回投げたとき、点Ｐが原点にある確率は
80/243　である。

どうして点Ｐが原点にある確率がこのようになったのか
解法を教えてください
お願い致します。
No.6027 - 2009/05/29(Fri) 22:36:15
☆ Re: 確率 / ヨッシー
確率で言うと、１回につき
　1/3 の確率で＋２、2/3の確率で−１です。
６回で原点に戻るのは、＋２が２回と、−１が４回です。
６回の内、どの２回を＋２にするかの選び方は
　6Ｃ2＝１５(通り)
それぞれについて
　1/3×1/3×2/3×2/3×2/3×2/3＝16/729
これに15を掛けて、80/243 となります。
No.6029 - 2009/05/29(Fri) 22:47:12
☆ Re: 確率 / ハオ
再度申し訳御座いません。僕自身の為でもあるのでお許しください。
(解答)
まず、点Pが６回の試行を終えた時に原点にある事を満たす為に正の向きに２移動する回数（事象A)が何回で負の向きに移動する回数(事象B)が何回かを求める必要があります。
tを用いて+2×t+(6-t)×-1=0という方程式は導けますか？
これを解いてt=2なので事象Aは２回事象Bは４回起これば良い事になります。
あとは反復試行の公式より
6C2×(1/3)^2　×(2/3)^4=80/243です。
No.6031 - 2009/05/29(Fri) 22:53:17
★ 平面上の問題です / hideki
どうも。初の投稿、失礼します。

平面上に、離れた点A,Bがあります。そして線分ABより十分短いことがわかっている定規があります。
この定規を用いて線分A,Bを結びたい。

これをパップスの定理を用いて証明してもらいたいのです。（パップスの定理は証明済みとします。ヒントとしては「パップスの定理の逆を用いる。」があります）
　　
　　　　よろしくお願いします。
No.6025 - 2009/05/29(Fri) 22:12:02
★ 極限 / aki
こんばんは！
また宜しくお願い致します(>_<)
http://w.upup.be/?2lFqm257L8
の問題なのですが、極限値をとるとき分子が0の条件を代入し、それから変形したところhttp://z.upup.be/?7S8KrbmT5h
までできましたが、それから後どうすればいいのかわかりません…
どなたか教えて下さい!
また少し前に質問しました極限の問題のご返答がいただけないので、どなたか教えて下さると有り難いです。宜しくお願いします！
No.6024 - 2009/05/29(Fri) 21:06:38
☆ Re: 極限 / だるまにおん
極限が有限となるためには、分子の
　lim[x→0](8+8b)/x
も有限でなければいけませんね。
No.6032 - 2009/05/29(Fri) 22:59:04
☆ Re: 極限 / aki
ごめんなさいなぜでしょうか（？＿？）
分子が8に収束するのが、分子のこの部分だけ0に収束するということに繋がるのが全くわかりません…
詳しく教えて下さい…
No.6035 - 2009/05/30(Sat) 16:09:35
☆ Re: 極限 / だるまにおん
> 分子が8に収束するのが、
分母は8に収束しますけど、分子が8に収束するとは限りませんね。

(8+8b)/x以外の部分はx→0のとき有限確定です：
　分母 → 8
　-b2 → -b2
　-14sin2x/x2 → -14

したがって、乱暴にいえば、x→0のとき
　与式→(-b2-lim[x→0](8+8b)/x-14)/8
ですね。よって、
　lim[x→0](8+8b)/x
が有限値に収束しなければ、与式も有限の値になりません。
No.6043 - 2009/05/30(Sat) 17:29:37
☆ Re: 極限 / aki
ごめんなさい…本当に分からないです…
極限の基礎的な考え方が分かっていないのかもしれません。
lim{x→∞}f(x)/G(x)=αと極限値をとる時
G(x)=0ならf(x)=0
という公式じみたものを暗記していただけなので…(>_<)
どうかお助け下さい、
No.6066 - 2009/05/31(Sun) 15:24:12
★ (No Subject) / りんご
2次方程式x^2+ax+12=0が異なる2つの実数解をもち、そのうち
の1つだけが2<x<3の範囲にあるように、定数aの値の範囲を
求めると、-8<a<-7　である。

どうして、定数aの値の範囲がこのようになったのか
解説を教えてください。
No.6016 - 2009/05/28(Thu) 23:35:57
☆ Re: / ハオ
僕の回答は無視して頂いても構いませんが、一応自分の為にとも思うので記しておきますね。
題意を満たすためには(グラフを書くと分かるのですが)
f(x)=x^2+ax+12 と置くと
f(2)<0かつf(3)>0 又は　f(2)>0かつf(3)<0を満たせばよい。
このままでは模試の時等は時間的に大変です。
二つの条件は　f(2)f(3)<0と同値であるのでこちらを考えます。
計算すると(a+8)(a+7)<0より
-8<a<-7
No.6017 - 2009/05/28(Thu) 23:46:08
☆ Re: / ヨッシー
ハオさんの回答で申しぶんありません。
「１つだけ」というのがミソですね。
２つ持ってもいい場合は、別の条件も必要になります。

>このままでは模試の時等は時間的に大変です。
これは８割方正しいですが、たとえばf(x) の中に
ａ^2 の項があったりすると、f(2)f(3) が４次式になったりしますので、
その場合は、個々の不等式を解いていくほうが良い場合もあります。
今にそういう問題にも出会うでしょう。
No.6022 - 2009/05/29(Fri) 08:21:45
☆ Re: / りんご
ハオさん、ヨッシーさん

おかげで分かりました

ありがとうございます。
No.6026 - 2009/05/29(Fri) 22:22:16
☆ Re: / ハオ
ヨッシーさんの補足は僕にとっても大変意義のあるものでした。深く感謝いたします。
No.6028 - 2009/05/29(Fri) 22:45:08
全22782件 [ ページ : << 1 ... 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064 1065 1066 1067 1068 1069 ... 1140 >> ]