ƒxƒNƒgƒ‹‚ح–³‚µ‚إ‚¨ٹè‚¢‚µ‚ـ‚·
گ³ژlٹpگچo-abcd‚ة‚آ‚¢‚ؤoa,
ob,oc,od,ٹe•س‚ة‚»‚ꂼ‚ê
op:oa‚ھa:1,oq:ob‚ھb:1,or:oc‚ھc:1,os:od‚ھd:1 ‚ئ‚ب‚é‚و‚¤‚ب“_p,q,r,s‚ًژو‚ء‚½‚ئ‚«a,b,c,d‚جٹضŒWژ®‚ًڈo‚¹
•½–تpqrs‚إگط’f‚µ‚ؤپAo‚©‚畽–تabcd‚ةگ‚گü‚ًˆّ‚«
•½–تoac,obd‚ًŒ©‚ؤچl‚¦‚½‚ج‚إ‚·‚ھپA‚±‚جگو‚ھŒ©‚¦‚ـ‚¹‚ٌ
‚و‚낵‚‚¨ٹè‚¢‚µ‚ـ‚·پB
|
No.5406 - 2009/03/08(Sun) 10:31:28
| پ™ Re: ’†ٹw‚ج—§‘جگ}Œ`‚ة‚آ‚¢‚ؤ / ژµ | | | > ƒxƒNƒgƒ‹‚ح–³‚µ‚إ‚¨ٹè‚¢‚µ‚ـ‚·
>
> گ³ژlٹpگچo-abcd‚ة‚آ‚¢‚ؤoa,
> ob,oc,od,ٹe•س‚ة‚»‚ꂼ‚ê
> op:oa‚ھa:1,oq:ob‚ھb:1,or:oc‚ھc:1,os:od‚ھd:1 ‚ئ‚ب‚é‚و‚¤‚ب“_p,q,r,s‚ًژو‚ء‚½‚ئ‚«a,b,c,d‚جٹضŒWژ®‚ًڈo‚¹
>
> •½–تpqrs‚إگط’f‚µ‚ؤپAo‚©‚畽–تabcd‚ةگ‚گü‚ًˆّ‚«
> •½–تoac,obd‚ًŒ©‚ؤچl‚¦‚½‚ج‚إ‚·‚ھپA‚±‚جگو‚ھŒ©‚¦‚ـ‚¹‚ٌ
> ‚و‚낵‚‚¨ٹè‚¢‚µ‚ـ‚·پB
ٹضŒW‚ح‚ب‚¢‚و‚¤‚ةژv‚¢‚ـ‚·پB–â‘蕶‚حگ³ٹm‚إ‚·‚©پH
‚ ‚ئپC‘ه•¶ژڑ‚حژg‚¦‚ب‚¢‚ج‚إ‚·‚©پH
|
No.5407 - 2009/03/08(Sun) 12:48:39 |
| پ™ Re: ’†ٹw‚ج—§‘جگ}Œ`‚ة‚آ‚¢‚ؤ / hiro | | | ‚·‚¢‚ـ‚¹‚ٌ”ن—¦ˆبٹO‚ح‚·‚ׂؤ‘ه•¶ژڑ‚ئچl‚¦‚ؤ‚‚¾‚³‚¢پB
‚ـ‚½–â‘è‚ة‚آ‚¢‚ؤ‚ح‚ ‚ء‚ؤ‚¢‚é‚©‚ا‚¤‚©‰ً‚è‚ـ‚¹‚ٌ‚ھ 1/a+1/cپپ1/b+1/d
‚ئ‚¢‚¤ژ®‚ھ‰½Œآ‚©‚ج‘S‚ؤ‚جگ³ژlٹpگچ‚ة‹¤’ت‚µ‚ؤŒ©‚ç‚ꂽ‚ج‚إ‚·‚ھ‚ا‚¤‚إ‚µ‚ه‚¤پH
|
No.5408 - 2009/03/08(Sun) 14:57:28 |
| پ™ Re: ’†ٹw‚ج—§‘جگ}Œ`‚ة‚آ‚¢‚ؤ / ژµ | | | > 1/a+1/cپپ1/b+1/d
‚ب‚؛‚±‚¤‚ب‚é‚ج‚©‚³‚ء‚د‚è•ھ‚©‚è‚ـ‚¹‚ٌپB
‘هژ–‚ب•”•ھ‚ھ”²‚¯‚ؤ‚¢‚é‚و‚¤‚ةژv‚¢‚ـ‚·پB
–â‘蕶‚ھگ³‚µ‚¢‚ب‚ç
•½–تPQRS‚ھڈo—ˆ‚é‚ئ‚حژv‚¦‚ـ‚¹‚ٌپB
|
No.5409 - 2009/03/08(Sun) 15:34:21 |
| پ™ Re: ’†ٹw‚ج—§‘جگ}Œ`‚ة‚آ‚¢‚ؤ / hiro | | | گ\‚µ–َ‚ ‚è‚ـ‚¹‚ٌپB
گ³‚µ‚‚ح–â‘蕶‚جچإŒم‚ة‚©‚ء‚±ڈ‘‚«‚إ
‚½‚¾‚µ•½–ت‚o‚p‚q‚r‚ح‚±‚جگ³ژlٹpگچ‚ًگط’f‚إ‚«‚é‚à‚ج‚ئ‚·‚éپB
‚ئپA‚ ‚è‚ـ‚·پB
—‰ً‚ھگَ‚‚ؤ‚·‚ف‚ـ‚¹‚ٌ‚±‚ê‚إ‘هڈن•v‚إ‚µ‚ه‚¤‚©پH
|
No.5410 - 2009/03/08(Sun) 16:28:51 |
| پ™ Re: ’†ٹw‚ج—§‘جگ}Œ`‚ة‚آ‚¢‚ؤ / ƒˆƒbƒVپ[  | | | 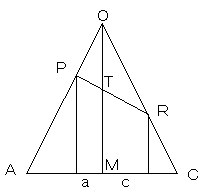
پ¢‚n‚`‚b‚ة‚¨‚¢‚ؤپA‚`‚b‚ج’†“_‚ً‚lپA‚n‚l‚ئ‚o‚q‚جŒً“_‚ً‚s‚ئ‚µپA
‚l‚ًŒ´“_‚ئ‚µ‚ؤپA‚`(-1,0)پA‚b(1,0)پA‚n(0,h) ‚ئ‚·‚é‚ئپA
‚o(-a, (1-a)h)پA‚q(c, (1-c)h) ‚ئ‚ب‚èپA‚o‚q‚ئ‚™ژ²‚l‚n‚ئ‚ج
Œً“_‚s‚حپA(0, h-2ach/(a+c))
پ¢‚n‚a‚c‚ة‚آ‚¢‚ؤ“¯—l‚ةچl‚¦‚é‚ئپA“_‚s‚جچہ•W‚ح
پ@(0, h-2bdh/(b+d))
‚±‚ج‚Q“_‚ح“¯‚¶“_‚ب‚ج‚إپA
پ@h-2ach/(a+c)پپh-2bdh/(b+d)
‚و‚èپA
پ@ac/(a+c)پپbd/(b+d)
‚ئ‚ب‚èپA 1/a+1/cپپ1/b+1/dپ@‚حٹm‚©‚ةگ¬‚è—§‚؟‚ـ‚·پB
|
No.5412 - 2009/03/09(Mon) 02:04:09 |
|

