この問題がわかりません。
Oを原点とする座標平面上に2点A(6,0)、B(0,6)があり、座標平面上を動く点Pが初め原点にある。次の(操作)を6回繰り返し行う。
(操作)2枚の硬貨を投げ、表が2枚出ればPをx軸の正の向きに1だけ動かし、表と裏が1枚ずつ出ればPをy軸の正の向きに1だけ動かし、裏が2枚出ればPを動かさない。
(操作)を6回行った後のPの位置について、問に答えよ。
(問)Pが三角形OABの内部にあり、かつ、三角形PABの面積が6以下である確率を求めよ。
|
No.75309 - 2021/06/01(Tue) 12:46:21
| ☆ Re: 格子 / ヨッシー  | | | 辺上の点は内部と見なさないとしています。
6回操作したあとのPの座標を(x, y) とすると、
0≦x, 0≦y, x+y≦6
であり、面積は
△OAP=OA×y÷2=3y
△OBP=OB×x÷2=3x
より
△PAB=△OAB−△OAP−△OBP=18−3(x+y)
これが6以下であるためには、
12≦3(x+y)
4≦x+y
よって、図の青い点が条件を満たす点となります。
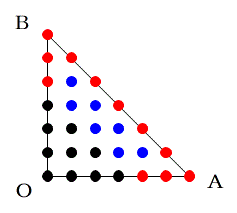
つまり、Pの座標が
(1, 3) (1, 4) (2, 2) (2, 3) (3, 1) (3, 2) (4, 1)
のときで、以下、確率を求めます。
表表が出る事象をR,表裏が出る事象をS,裏裏が出る事象をTとします。
一回あたりの確率は Sが1/2、RとTが1/4ずつです。
(1, 3):RSSSTTの並び替えが 6C1×5C2=60 確率が 1/512
(1, 4):RSSSSTの並び替えが 6C1×5C1=30 確率が 1/256
(2, 2):RRSSTTの並び替えが 6C2×4C2=90 確率が 1/1024
(2, 3):RRSSSTの並び替えが 6C1×5C2=60 確率が 1/512
(3, 1):RRRSTTの並び替えが 6C1×5C2=60 確率が 1/2048
(3, 2):RRRSSTの並び替えが 6C1×5C2=60 確率が 1/1024
(4, 1):RRRRSTの並び替えが 6C1×5C1=30 確率が 1/2048
よって、求める確率は
60/512+30/256+90/1024+60/512+60/2048+60/1024+30/2048
=30/256+120/512+150/1024+90/2048
=240/2048+480/2048+300/2048+90/2048
=1110/2048
=555/1024
|
No.75312 - 2021/06/01(Tue) 14:21:32 |
| ☆ Re: 格子 / アーモンド | | | ありがとうございます。余事象を使わずに解く方法もあるのですね。
|
No.75313 - 2021/06/01(Tue) 14:31:18 |
| ☆ Re: 格子 / ヨッシー  | | | あ、余事象の方が良いのかなぁ。
でも思いつかなかったので。
思いついたのが、いい方法。
私のモットーです。
|
No.75321 - 2021/06/01(Tue) 16:44:31 |
|

