よろしくお願いします
![]() |
No.74943 - 2021/05/24(Mon) 21:37:03
| ☆ Re: / ヨッシー  | | | (1)
f(0)=b, f(1)=a+b+1 なので、
2f(1)−f(0)=2a+b+2
よって、
f(2)=2a+b+4=2f(1)−f(0)+2
(2)
f(0), f(1), f(2) のいずれもが絶対値が1/2未満とすると
f(0)−2f(1)+f(2)=2
において、
-1/2<f(0)<1/2
-1<−2f(1)<1
-1/2<f(2)<1/2
より
−2<f(0)−2f(1)+f(2)<2
となり、
f(0)−2f(1)+f(2)=2
となり得ない。
よって、f(0), f(1), f(2) のうち少なくとも1つは絶対値が1/2以上。
(3)
y=x^2+ax+b のグラフを考えると、
f(0), f(1), f(2) の1つだけ絶対値が1/2 以上で、残り2つの絶対値が 1/2 より小さい
というのは
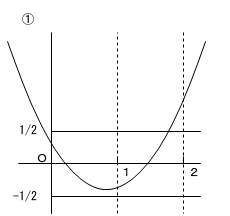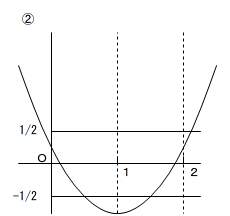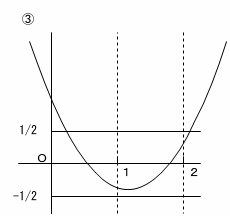
この3通りです。
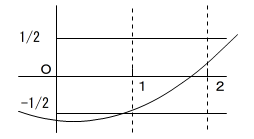
このようにはなりません。
この図では、頂点はx<1 の範囲にあり、グラフの頂点より右だけをみると、
xが1増えるときのyの増加量は1より大きくなり、f(1), f(2) の両方が
-1/2<y<1/2
に入ることはないからです。
さて、上の図の、?@?A?Bの順に不等式を作っていきます。
f(0)=b, f(1)=a+b+1, f(2)=2a+b+4
を確認しておきます
?@ |f(2)| のみ 1/2以上
-1/2<b<1/2
-1/2<a+b+2<1/2
1/2≦2a+b+4
?A |f(1)| のみ 1/2 以上
-1/2<b<1/2
a+b+2≦-1/2
-1/2<2a+b+4<1/2
?B |f(0)| のみ 1/2 以上
1/2≦b
-1/2<a+b+2<1/2
-1/2<2a+b+4<1/2
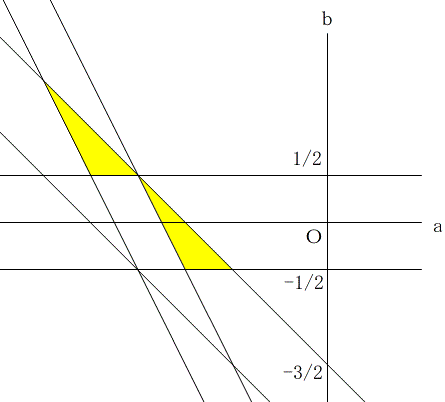
以上より、図の黄色の部分が対象の範囲となります。
?Aを満たす範囲はありません。
|
No.74978 - 2021/05/25(Tue) 12:15:38 |
| ☆ Re: / 大阪太郎 | | | 図形と方程式と背理法の融合問題なんてあまり見たことがなく斬新な問題だと思いました。 ありがとうございました。
|
No.74979 - 2021/05/25(Tue) 12:54:52 |
|