高校2年です。
次の問題を教えて下さい。
空間の4点O(0,0,0),A(1,0,0),B(0,1,0),C(0,0,1)を頂点とする四面体に含まれ、中心軸がz軸と平行な直円柱のうち、体積が最大になるものの底面の半径と高さ、およびその最大値を求めよ。
どうぞよろしくお願いします。
|
No.72183 - 2021/01/18(Mon) 01:56:05
| ☆ Re: 空間座標 / ヨッシー  | | | 直円柱の底面の半径をrとします。
底面をxy平面上でx軸とy軸の両方に接するように置き
高さを最大まで延ばした時を考えます。
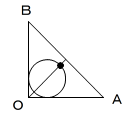
図の、点((1+√2)r,(1+√2)r,0)をz軸方向に伸ばして、
3点A,B,Cを通る平面 x+y+z=1 に触れるまでが
高さの最大です。
この時の高さは
z=1−x−y=1−2(1+√2)r 0<r<1−1/√2
直円柱の体積Vは
V=πr^2{1−2(1+√2)r}=π{r^2−2(1+√2)r^3}
rで微分して
dV/dr=π{2−6(1+√2)r}r
よって、r=0で極小、r=(√2−1)/3 で極大となります。
(以下略)
|
No.72185 - 2021/01/18(Mon) 06:57:44 |
| ☆ Re: 空間座標 / X | | | 直円柱の底面の円の半径ではなくて、
高さを固定した場合の別解の方針を。
問題の円柱の高さをhとして
点O'(0,0,h)
を取ります。
今、3点A,B,Cを通る平面が
x+y+z=1 (A)
であることに注意すると、(A)と
平面z=hとの交線の方程式は
z=h,x+y+h=1 (B)
∴(A)(B)とzx平面、yz平面との交点を
A',B'に取ると、
A'(1-h,0,h),B'(0,1-h,h)
となるので、hを固定したとき、
問題の直円柱の底面の円
の半径が最大となるとき、その円は
△OA'B'の内接円
となっています。
よってこの円の半径をrとすると、
△ABCの面積について
(1/2)r{2(1-h)+(1-h)√2)}=(1/2)(1-h)^2
これより
r=(2-√2)(1-h)/2
∴このときの直円柱の体積をVとすると
V=h・πr^2=π{(3-2√2)/2}h(1-h)^2
=π{(3-2√2)/2}(h^3-2h^2+h)
後はdV/dhを求めて、0<h<1の範囲で
Vについての増減表を書きます。
|
No.72187 - 2021/01/18(Mon) 17:30:42 |
| ☆ Re: 空間座標 / らすかる | | | 直円柱を固定して平面を動かす別解(微分は使っていません)
直円柱を固定し、A(t,0,0),B(0,t,0),C(0,0,s)(t>2)とおいて
平面ABCと直円柱の接点を(1,1,1)とすると
x/t+y/t+z/s=1が(1,1,1)を通ることからs=t/(t-2)
全体を縮小してA(1,0,0),B(0,1,0),C(0,0,1)となるようにすると
x方向とy方向が1/t倍、z方向が(t-2)/t倍なので
直円柱の体積は(t-2)/t^3倍になる。
(t-2)/t^3=kとおいて整理し、3変数の相加相乗平均を適用すると
1=kt^2+1/t+1/t≧3[3]√kとなるから
kの最大値は1/27となり、そのときkt^2=1/tからt=3
よって平面ABCと直円柱の接点が(1/t,1/t,(t-2)/t)=(1/3,1/3,1/3)
のときに直円柱の体積が最大となるから、
直円柱の底面の半径が(2-√2)/3、高さが1/3のときに
体積が最大値2π(3-2√2)/27となる。
ヨッシーさんの解答ともXさんの解答とも合わないのでいろいろ確認したのですが、
> ヨッシーさん
> 図の、点((1+√2)r,(1+√2)r,0)をz軸方向に伸ばして、
これは点((2+√2)r/2,(2+√2)r/2,0)ではありませんか?
> Xさん
> △ABCの面積について
> (1/2)r{2(1-h)+(1-h)√2)}=(1/2)(1-h)^2
> これより
> r=(√2-1)(1-h)/2
(1/2)r{2(1-h)+(1-h)√2)}=(1/2)(1-h)^2 を変形すると
r=(2-√2)(1-h)/2 になりませんか?
# もし私の勘違いでしたらご容赦下さい。
# ヨッシーさんとXさんの答えが一致しているので、いくら確認しても不安…
|
No.72189 - 2021/01/18(Mon) 18:43:22 |
| ☆ Re: 空間座標 / R | | | ヨッシー様
X様
らすかる様
皆さんありがとうございます。
らすかる様のご指摘下さった通り、
点の座標が(r+r/√2,r+r√2,0)で体積を計算したところ、
V=πr^2{1-(2+√2)r}
V'=πr{2-(6+3√2)r}
でr=(2-√2)/3のとき、らすかる様の答えと一致致しました!
沢山の別解ありがとうございます。
じっくり勉強致します!
|
No.72193 - 2021/01/18(Mon) 19:40:29 |
| ☆ Re: 空間座標 / ヨッシー  | | | らすかるさん
いえ、こちらが間違っています。
Rさん
らすかるさんの答えと合ってよかったです。
|
No.72195 - 2021/01/18(Mon) 20:09:46 |
| ☆ Re: 空間座標 / X | | | >>らすかるさんへ
ご指摘ありがとうございます。
>>Rさんへ
ごめんなさい。らすかるさんの仰る通りです。
No.72187を直接修正しましたので再度ご覧下さい。
|
No.72199 - 2021/01/18(Mon) 22:07:14 |
| ☆ Re: 空間座標 / R | | | No.72226 - 2021/01/19(Tue) 22:42:06 |
|


