分からないので、教えてください。
![]() |
No.63157 - 2020/01/21(Tue) 21:06:28
| ☆ Re: 中1数学 / 円 | | | こっちが(1)、(2)です。
![]() |
No.63158 - 2020/01/21(Tue) 21:14:54 |
| ☆ Re: 中1数学 / ヨッシー  | | | (3) だけでいいのかな?
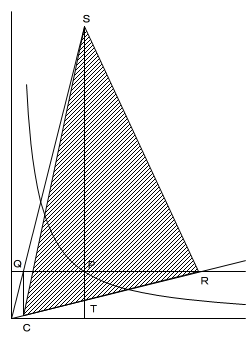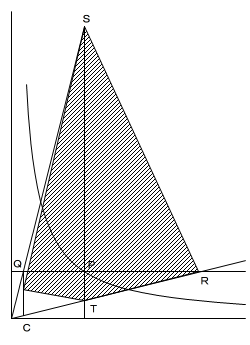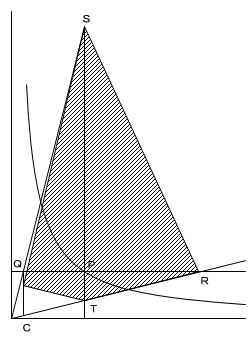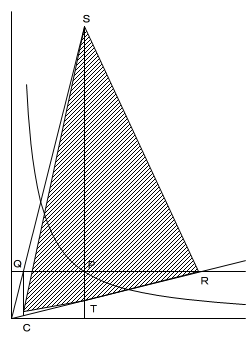
(3)
△AST=△BST より、STを底辺としたときの
高さが等しくなるためには、STが点A,点Bから等距離に
なければならないので、点Pのx座標(点S、点Tも同じ)は、
AとBのx座標の真ん中で、x=5です。
四角形QTRSと△CRSにおいて、△STRは共通なので、
△QSTと△CSTの面積が等しければ、
四角形QTRS=△CRS
となります。
点QをSTに平行に直線?A上まで動かした点がCなので、
P(5, 16/5)、Q(4/5, 16/5)、C(4/5, 1/5)
の順に求められます。
|
No.63159 - 2020/01/21(Tue) 21:38:42 |
| ☆ Re: 中1数学 / 円 | | | ごめんなさい、(1)、(2)もお願いします。
> (3) だけでいいのかな?
>
> (3)
> △AST=△BST より、STを底辺としたときの
> 高さが等しくなるためには、STが点A,点Bから等距離に
> なければならないので、点Pのx座標(点S、点Tも同じ)は、
> AとBのx座標の真ん中で、x=5です。
> 四角形QTRSと△CRSにおいて、△STRは共通なので、
> △QSTと△CSTの面積が等しければ、
> 四角形QTRS=△CRS
> となります。
> 点QをSTに平行に直線?A上まで動かした点がCなので、
> P(5, 16/5)、Q(4/5, 16/5)、C(4/5, 1/5)
> の順に求められます。
>
|
No.63160 - 2020/01/21(Tue) 22:56:40 |
| ☆ Re: 中1数学 / ヨッシー  | | | (1)
?Bは反比例の式なので、
y=a/x
の形の式になります。これが点A(2, 8)を通るので、
y=16/x
(2)
Pの座標は、y=16/x にx=3を代入して y=16/3 より
(3, 16/3)
y=16/3 に対応する ?@y=4x 上の点Qは Q(4/3, 16/3)
x=3 に対応する ?@y=4x 上の点Sは S(3, 12)
点Bは(8, 2) なので、?A の式は y=x/4
y=16/3 に対応する ?Ay=x/4 上の点Rは R(64/3, 16/3)
x=3 に対応する ?Ay=x/4 上の点Tは T(3, 3/4)
四角形QTRS=(1/2)QR・ST
=(1/2)20・(45/4)=225/2
|
No.63162 - 2020/01/21(Tue) 23:37:33 |
| ☆ Re: 中1数学 / 円 | | | No.63185 - 2020/01/23(Thu) 23:03:51 |
|

