この問題を教えてください
BC=2, ∠A=π/2の三角形ABCがある。直線BCに関してAと対称な点をDとし、点EをAC(ベクトル)=BE(ベクトル)を満たすようにとる。また、直線BEと直線CDの交点をGとする。AC>BCを満たすように三角形ABCを動かすとき、三角形AFGの面積を最大にするtan^2(∠ACB)の値を求めよ。
|
No.49336 - 2018/03/20(Tue) 15:01:10
| ☆ Re: 三角比とベクトル / ヨッシー  | | | BCは直角三角形ABCの斜辺なので
AC>BC
にはなり得ません。
また、点Fが定義されていません。
|
No.49337 - 2018/03/20(Tue) 15:16:33 |
| ☆ Re: 三角比とベクトル / ぱっぱ | | | AC>ABでした
また、点FとはBEとADの交点であります
|
No.49340 - 2018/03/20(Tue) 16:15:48 |
| ☆ Re: 三角比とベクトル / ヨッシー  | | | 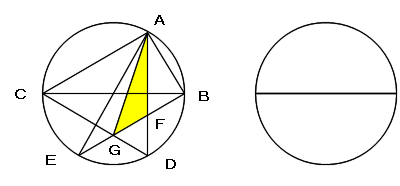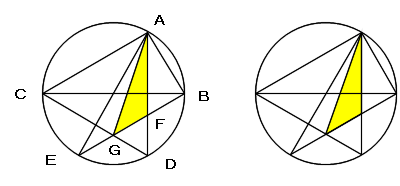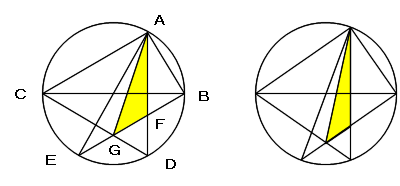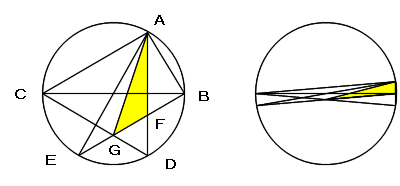
∠ACB=θ (0<θ<π/4) とおくと ∠AOB=2x (OはBCの中点)であるので、
A(cos2θ, sin2θ)、B(1, 0)、C(-1, 0)
D(cos2θ, −sin2θ)、E(−cos2θ, −sin2θ)
と表せます。
EBの式は
y=sin2θ(x−1)/(1+cos2θ)
Fはこの直線上でAとx座標が同じ点であるので、Fのy座標Fyは
Fy=sin2θ(cos2θ−1)/(1+cos2θ)
AFの長さは
AF=sin2θ−sin2θ(cos2θ−1)/(1+cos2θ)
=2sin2θ/(1+cos2θ)
△AFGにおいて、AFを底辺としたときの高さは、
Aのx座標の cos2θ であるので、
△AFG=cos2θ・sin2θ/(1+cos2θ)
=sin4θ/2(1+cos2θ)
f(θ)=sin4θ/2(1+cos2θ) と置きます。θで微分して
f'(θ)={2cos4θ(1+cos2θ)+sin2θsin4θ}/(1+cos2θ)^2
(分子)=2(2cos^2(2θ)−1)(1+cos2θ)+2sin^2(2θ)cos2θ
=2(2cos^2(2θ)−1)(1+cos2θ)+2{1−cos^2(2θ)}cos2θ
=2{2cos^2(2θ)−1+2cos^3(2θ)−cos2θ+cos2θ−cos^3(2θ)}
=2{cos^3(2θ)+2cos^2(2θ)−1}
=2(cos2θ+1)(cos^2(2θ)+cos2θ−1)
0<2θ<π/2 より 0<cos2θ<1
この範囲で (分子)=0 を解くと
cos2θ=(√5−1)/2
2cos^2θ−1=(√5−1)/2
cos^2θ=(√5+1)/4
tan^2θ=(1/cos^2θ)−1 より
tan^2∠ACB=√5−2 ・・・答
|
No.49361 - 2018/03/21(Wed) 19:11:03 |
|
