ヨッシーの八方掲示板（小中高の算数・数学　質問掲示板）

★ 整数の性質 / 高校1年生

この問題の解き方がわかりません
教えてくださいお願いします。

No.47369 - 2017/12/20(Wed) 16:42:49

☆ Re: 整数の性質 / ヨッシー

100a＋10b＋7＝・・・　はただの式変形ですので、ａ，ｂの係数が合うようにア、イを決めます。
ウは７です。

ａ，ｂが素数の時、ａ，ｂは２，３，５，７のいずれか(重複も可)なので、
上で求めたア、イを使った、アａ＋イｂに、順に当てはめていって、７で割れるかを
調べます。結果、７で割れるのは、
　（ａ，ｂ）＝（３，５）、（７，７）
だけで、エオカ、キクケは３５７，７７７となります。
　３５７×７７７＝５１×１１１×７^2
であり、５１×１１１＝５６６１を７進法で表すと
　５６６１÷７＝８０８　あまり　５
　８０８÷７＝１１５　あまり　３
　１１５÷７＝１６　あまり　３
　１６÷７＝２　あまり　２
より　５６６１(10)＝２２３３５(7)
なので、コサシスセソタ　は　２２３３５００(7) となります。

No.47370 - 2017/12/20(Wed) 17:23:28

☆ Re: 整数の性質 / 高2

ヨッシーさん解説ありがとうございました！

No.47373 - 2017/12/21(Thu) 03:58:02

★ (No Subject) / 寒い

一辺の長さが1の立方体ABCD-EFGHがある。辺EF上に点Pをとる。頂点B,Dおよび点Pを含む平面によって立方体を2つの立体に切断する時頂点Aを含む立体の体積をV1,頂点Gを含む体積をV2とする。V1;V2=1:√2が成り立つ

この時?@EP,?AtanABP,?BBPの値を求めよ

答え?@=(√5−1)/2 ?A（√5＋3)/2 ?B√3(√5＋1)/2
答えしか乗ってなくて模範解答ないので困っています。やり方教えてください。お願いします

No.47367 - 2017/12/20(Wed) 16:01:15

☆ Re: / ヨッシー

?@＝(√5−1)/2 だと、V1:V2=1:2 になると思いますが。

No.47371 - 2017/12/20(Wed) 18:24:54

☆ Re: / ヨッシー

Ｖ１：Ｖ２＝１：２とすると、以下のように、全部答えと合います。

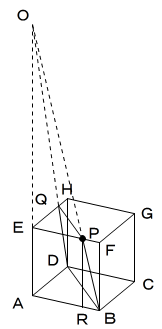
切断面とＡＤの交点をＱとすると、
　ＰＱ//ＢＤ　ＥＰ＝ＥＱ
が成り立ちます。

　ＥＰ＝ＥＱ＝ｘ　（０＜ｘ＜１）
とおき、ＢＰ．ＤＱ，ＡＥの交点をＯとします。
　ＯＥ：ＯＡ＝ｘ：１
であるので、
　ＯＡ＝1/(1－x)
三角すいＯ－ＡＢＤの体積は　1/6(1－x)
三角すいＯ－ＥＰＱの体積は、そのｘ^3倍で、ｘ^3/6(1－x)
よって、
　Ｖ1＝(1－ｘ^3)/6(1－x)＝(x^2＋x＋1)/6
これが、立方体ＡＢＣＤ－ＥＦＧＨの　1/3 倍になるので、
　(x^2＋x＋1)/6＝1/3
　x^2＋x＋1＝2
　x^2＋x－1＝0
これを解いて、
　ｘ＝(－1＋√5)/2
このとき、ＰからＡＢに下ろした垂線の足をＲとすると、
　tan∠ＡＢＰ＝ＲＰ/ＢＲ＝1/(1－x)
ここで
　1－x＝(3－√5)/2
なので
　tan∠ＡＢＰ＝2/(3－√5)＝(3＋√5)/2
また、
　ＢＰ＝√(ＰＲ^2＋ＢＲ^2)＝√{1＋(1－x)^2}
ここで、
　1＋(1－x)^2＝1＋(7＋3√5)/2＝(9＋3√5)/2
　　＝3(6＋2√5)/4＝(3/4)(√5＋1)^2
よって、
　ＢＰ＝(√3/2)(√5＋1)

No.47372 - 2017/12/20(Wed) 18:36:22

★ 三角 / 高1

三角形ABCがり、AB=√2,BC=3√3,CA=5とする。
この画像の問題がわかりません。
解説をお願いします。

No.47364 - 2017/12/20(Wed) 14:01:41

☆ Re: 三角 / ヨッシー

△ＡＢＣは∠Ａ＝90°の直角三角形であり、
　cos∠Ｂ＝√2/3√3
△ＡＣＤにおける余弦定理より
　ＡＣ^2＝ＡＤ^2＋ＣＤ^2－２ＡＤ・ＣＤcos∠ＡＤＣ
∠ＡＤＣ＝∠ＡＢＣより
　２５＝９＋ｘ^2－６(√2/3√3)ｘ
　ｘ^2－(2√6/3)ｘ－１６＝０　　　・・・エオカ
これをｘ＞０で解いて
　ｘ＝2√6　　　・・・キク
△ＢＣＤにおける三平方の定理より
　ＢＤ＝√3
よって、
　△ＡＢＣ＝5√2/2
　△ＢＣＤ＝3√2
よって、
　四角形ＡＢＤＣ＝11√2/2　・・・ケコサシ
ＤＰ：ＰＡ＝△ＢＣＤ：△ＡＢＣ＝６：５　より
　ＡＰ＝15/11
△ＡＢＰにおける正弦定理より
　ＡＢ/sin∠ＡＰＢ＝ＡＰ/sin∠ＰＢＡ
　sin∠ＡＰＢ＝ＡＢsin∠ＰＢＡ/ＡＰ
　　＝√2(5/3√3)/(15/11)
　　＝11√6/27

No.47366 - 2017/12/20(Wed) 14:52:02

☆ Re: 三角 / 高1

ヨッシーさん
図まで書いていただいてありがとうございます。
とてもわかりやすかったです！

No.47368 - 2017/12/20(Wed) 16:37:51

★ (No Subject) / 七

この問題の解き方が分かりません。教えてください。よろしくお願いします。(1)はB'(－1,－2,
－1)で(2)はP(－1,1/2,1)で最小値は√41です。

No.47360 - 2017/12/20(Wed) 00:27:39

☆ Re: / らすかる

(1)
πの式はx+2y+2z=2なので法線ベクトルの一つは(1,2,2)
Bを通りπに垂直な直線は(1,2,3)+t(1,2,2)=(1+t,2+2t,3+2t)とおける
x=1+t,y=2+2t,z=3+2tをπの式に代入してtを求めるとt=-1
よってB'の座標は(1,2,3)+(-2)(1,2,2)=(-1,-2,-1)
(2)
AP+PBの最小値は線分AB'の長さなので
√{(-1+1)^2+(3+2)^2+(3+1)^2}=√41
Pは直線AB'とπの交点なので
直線AB'をA+s(B'-A)=(-1,3,3)+s(0,-5,-4)=(-1,3-5s,3-4s)とおいて
πの式に代入しsを求めるとs=1/2
従って直線AB'の式にs=1/2を代入してP=(-1,1/2,1)

No.47361 - 2017/12/20(Wed) 01:02:35

★ 体積比、教えてください! / 中3

正四面体ABCDがあり点E,Fはそれぞれ辺AB,ACの中点,点GはAG:GD=2:1となる点である。このとき、E,B,C,F,Gを頂点とする立体の体積は、正四面体ABCDの体積の何倍か。
答えは1/2です。解き方を教えて下さい。

No.47353 - 2017/12/19(Tue) 19:53:15

☆ Re: 体積比、教えてください! / ヨッシー

四面体ＡＥＦＧの体積は、ＡＥＦを底面とすると、
　底面はＡＢＣＤの1/4倍
　高さは、2/3 倍
　体積は 1/4×2/3＝1/6 倍
四面体ＧＢＣＤの体積は、底面ＢＣＤは共通で、
　高さは 1/3 倍なので、体積も 1/3倍。
残りが求める立体の体積なので、
　1－1/6－1/3＝1/2（倍）

No.47354 - 2017/12/19(Tue) 19:57:15

☆ Re: 体積比、教えてください! / らすかる

別解
底面をABCの面とすると、
四角錐G-BCFEは三角錐D-ABCと比較して
底面積が3/4倍、高さが2/3倍なので
四角錐G-BCFEの体積は三角錐D-ABCの体積の
(3/4)×(2/3)=1/2倍となります。

No.47356 - 2017/12/19(Tue) 20:01:12

☆ Re: 体積比、教えてください! / 中3

ヨッシーさん、らすかるさん分かりやすい解説ありがとうございました!

No.47357 - 2017/12/19(Tue) 20:36:02

★ 大小関係がわかりません / 枕草子

3-√6と2-√2の大小を考えるときどうすればいいですか？
近似値を覚える必要があるんですか？

どっちが大きいか小さいかがわからなくてセンターIAの不等式の問題でミスしてしまいました。。

No.47349 - 2017/12/19(Tue) 14:09:51

☆ Re: 大小関係がわかりません / IT

√6をなくします。

3-√6と2-√2　移項して
1+√2 と　√6　二乗して
3+2√2 と 6　ここで判定する（√2 < 1.5を使って）か、移項して
2√2 と　3 ここで判定するか、2乗して
8 < 9

No.47351 - 2017/12/19(Tue) 15:44:50

★ 二次関数の問題です。 / 高校三年

aを定数ととし、2次関数y=x^2-(2a-2)x-2a+9…?@のグラフをGとする。
問1. Gの頂点の座標を求めよ。
問2. Gが(7,8)を通る時のaの値を求めよ。
問3. aの値によらず、Gはつねに点Pを通る。点Pの座標を求めよ。
問4. a>0とする。?@においてすべての実数xに対してy>0となるときのaの値の範囲を求めよ。
問5. a>0とし、すべての整数xに対してy>0となるときのaの値の範囲を求めよ。

問1～問4は解けましたが、問5の解き方がわかりません。解説には以下のようにあったのですが、意味が理解できませんでした、教えていただきたいです。

以下問5の解説

すべての整数xに対してy>0となるのは、軸x=a-1に最も近い整数xに対してy>0となるときである。
a>0よりa-1>-1であることから、
x=-1のときy=8>0
x＝0のときy=9-2a>0よりa<9/2…?A
x=1のときy=12-4a>0よりa<3…?B
x=2のときy=17-6a>0よりa<17/6…?C
?A,?B,?Cの共通範囲を求めるとa<17/6であり、このとき、軸x=a-1<11/6<2であるから、x≧3のときy>0である。
よって、0<a<17/6

以上

なぜx=0,1,2のときを調べると答えが出るのでしょうか…？
初歩的な質問で申し訳ありませんが、どうぞよろしくお願いします。

No.47345 - 2017/12/19(Tue) 00:55:58

☆ Re: 二次関数の問題です。 / らすかる

0,1,2のときでなく
「-1」「0」「1」「2」「3以上」
について調べていますね。
a＞0からa-1＞-1すなわち軸の位置がx＞-1なので
-1以上の整数について調べれば十分です。

No.47346 - 2017/12/19(Tue) 01:28:11

☆ Re: 二次関数の問題です。 / 高校三年

すみません…。
なぜ軸のx座標がx=1とx=2の間にあるとわかるのでしょうか…？
x=-1とx=0の間もしくはx=0とx=1の間ではないというのは、どこからわかるのですか？

No.47348 - 2017/12/19(Tue) 13:58:06

☆ Re: 二次関数の問題です。 / らすかる

「軸のx座標がx=1とx=2の間にある」という文は私には見つけられませんが、
どこかに書いてあったのですか？

No.47350 - 2017/12/19(Tue) 15:27:18

☆ Re: 二次関数の問題です。 / 高校三年

解説に図で示してありました。

No.47352 - 2017/12/19(Tue) 18:36:33

☆ Re: 二次関数の問題です。 / らすかる

その図は単なる例であって、
「軸のx座標がx=1とx=2の間にある」わけではないですね。
実際、答えが0＜a＜17/6ということは
軸はx=a-1から-1＜x＜11/6の範囲にあるわけですから、
aの値によっては-1と0の間、0と1の間にもあります。

No.47355 - 2017/12/19(Tue) 19:57:39

☆ Re: 二次関数の問題です。 / 高校三年

なるほど…！今理解できました。
長々とすみません。ありがとうございました！

No.47359 - 2017/12/19(Tue) 23:06:06

★ (No Subject) / るいと

a^2+b^2(a,bは整数)が3で割り切れる時、a,bはともに3で割り切れることを示せ。

これは、どのようにするのでしょうか。
対偶を示すのですか？
示すなら、その対偶は何ですか？

No.47341 - 2017/12/18(Mon) 19:06:27

☆ Re: / IT

対偶を示せばいいと思います。

（対偶）
整数a,b の少なくとも1つが３で割り切れないとき、a^2+b^2は３で割り切れない。

なお a^2+b^2はa,bについて対称なので、aが３で割り切れないときを考えればよいです。

No.47342 - 2017/12/18(Mon) 20:02:08

★ (No Subject) / サトル

2n＋1で割る理由教えて下さい。

No.47339 - 2017/12/18(Mon) 18:10:01

☆ Re: / X

添付されている画像に表示されている参考書？の中で
ご質問の式以降の行を一通り
(つまりご質問の問題の解説全て)
読みましたか？
その上で分からないのであれば、
再度その旨をアップして下さい。

No.47340 - 2017/12/18(Mon) 18:56:24

☆ Re: / X

No.47340 - 2017/12/18(Mon) 18:56:24

★ (No Subject) / サトル

2n＋1で割る理由教えて下さい。

No.47339 - 2017/12/18(Mon) 18:10:01

☆ Re: / X

No.47340 - 2017/12/18(Mon) 18:56:24

☆ Re: / X

No.47340 - 2017/12/18(Mon) 18:56:24

★ Re: Re:有機化学　正四面体 / 前進

頂点のＣＯＯＨは固定でＨＯ　ＣＨ^3 Ｈ(回転するらしいです)の場所がなぜ画像のようになるのかがわかりません。

それと🄫をどこに設定するとそれぞれの頂点方向に向かっているのかがわかりません。

よろしくお願いいたします。

No.47334 - 2017/12/18(Mon) 01:45:02

☆ Re: Re:有機化学　正四面体 / 前進

今、考えておりましたが前半は顕微鏡のレボルバーのようにすれば点が一致したので理解できました。

後半をよろしくお願いいたします。

尚前半もほかの考え方があればよろしくお願いいたします。

No.47335 - 2017/12/18(Mon) 01:49:47

☆ Re: Re:有機化学　正四面体 / angel

えっと、質問とあっているかは分かりませんが…。

まず基礎としてはメタン ( CH4、詳細はwikipediaの記事を参照のこと ) の配置がありまして。
正四面体の中心 ( 重心 ) に炭素原子が、正四面体の各頂点に水素原子が来る配置となります。

もし具体的に座標を知りたい、ということなら、もちろんどこにどう置くかで変わるのですが、一例として
C:原点、H:(0,0,1),(2√2/3,0,-1/3),(-√2/3,√6/3,-1/3),(-√2/3,√6/3,-1/3)

で、この問題の乳酸の場合。接続されているものが違うので、ぴったり正四面体というわけではないのですが、メタンの場合と似た、正四面体のような配置になりますよ、という話になっています。

No.47337 - 2017/12/18(Mon) 10:55:53

☆ Re: Re:有機化学　正四面体 / 前進

返信遅れて申し訳ありません。wikipediaの記事を見ると頂点へは長さがすべておなじでした。

C:原点、H:(0,0,1),(2√2/3,0,-1/3),(-√2/3,√6/3,-1/3),(-√2/3,√6/3,-1/3)　ちょっとまだ数学が理解できてないですが図から重心は底面からある高さのところにあることが分かったので、今回は一応これで終わりとして、数学をした後にもう一度考えてみます。
ありがとうございました

No.47414 - 2017/12/23(Sat) 12:51:20

★ 指数対数 / 高2

この問題の解答がわかりません
解説をお願いします。

No.47330 - 2017/12/17(Sun) 16:21:35

☆ Re: 指数対数 / ヨッシー

　s＝log[2]ｘ
において、ｘ＞１であるので、ｓ＞０　・・・ア
　log[2]Ａ＝log[2](x^3・y^4)＝log[2]x^3＋log[2]y^4
　　　＝3log[2]x＋4log[2]y＝3s＋4t　　・・・イウ
また、
　(4y)^(log[8]x)＝2
より
　log[8]x＝log[4y]2
　log[2]x/log[2]8＝log[2]2/log[2]4y
　s/3＝1/(t＋2)
　s(t＋2)＝3　　・・・エオ
ｓ＞０より
　t＋2＝3/s
　t＝3/s－2
これを、
　log[2]Ａ＝3s＋4t
に代入して、
　log[2]Ａ＝3s＋4(3/s－2)
　　　　＝3s＋12/s－8　・・・カキクケ

No.47336 - 2017/12/18(Mon) 10:32:41

☆ Re: 指数対数 / 高2

ヨッシーさんありがとうございます。
解決できました。
復習します。

No.47347 - 2017/12/19(Tue) 04:16:32

★ 整数問題 / Gaba

nを自然数とする。(2+√3)^nの整数部分が奇数であることを示せ。
わかる方お願いします。

No.47324 - 2017/12/16(Sat) 22:34:17

☆ Re: 整数問題 / angel

うーん…。高校範囲でしょうか。
ノーヒントだと厳しいような気もしますが、次のヒントがあれば行けるでしょうか。

* 数列 a[n] を a[n]=(2+√3)^n+(2-√3)^n と定義する
* 数列 a[n] は a[n]=4a[n-1]-a[n-2] ( n≧3 ) を満たす
* 数列 a[n] は n≧1 において常に偶数である ← 帰納法で
* (2+√3)^n=a[n]-(2-√3)^n により、この整数部分は奇数である ← (2-√3)^n の大きさが結構小さいことに着目

No.47325 - 2017/12/16(Sat) 22:45:42

☆ Re: 整数問題 / らすかる

(2+√3)^n+(2-√3)^nが偶数であることは
二項定理でも言えますね。

No.47327 - 2017/12/16(Sat) 23:02:31

★ 固有ベクトル / take

A =
| 1 2 0 |
| -1 5 1 |
| 0 -1 1 |
の固有値、固有ベクトルを求めなさい

という問題なのですが、
固有値は1, 2, 4であると求まりました。
固有値が1の場合を考えたときに、固有ベクトルが0になってしまい、困っています。
そのようなことはあり得ますか？
計算ミスでしょうか？

No.47318 - 2017/12/16(Sat) 15:34:36

☆ Re: 固有ベクトル / X

固有値1に対する固有ベクトルを
(x,y,z)
とすると、条件から
2y=0 (A)
-x+4y+z=0 (B)
-y=0 (C)
(A)(B)(C)より
y=0,z=x
∴固有ベクトルは
(1,0,1)
です。

No.47321 - 2017/12/16(Sat) 19:52:37

☆ Re: 固有ベクトル / take

ありがとうございます。
解決の方法が理解できました。

λ=1に属する固有ベクトルvを(x,y,z)とおく
Av=λvより
y=0
x-4y-z=0
自由度は1より
0以外の任意の実数tを使い
x=tとおくと
z=t
よって、

v=t(1,0,1)
但しtは0以外の実数

No.47326 - 2017/12/16(Sat) 23:01:39