質問させて頂きます
2等辺三角形で2辺の長さと2点の座標が分かっています
残りの1点の座標を求める方法(式)を教えて下さい
求めたいのは図のCの点になります
宜しくお願いします
|
No.42781 - 2017/04/13(Thu) 19:46:25
| ☆ Re: 2等辺三角形の点座標 / きゅう | | | 添付を忘れました
![]() |
No.42782 - 2017/04/13(Thu) 19:46:52 |
| ☆ Re: 2等辺三角形の点座標 / ヨッシー  | | | 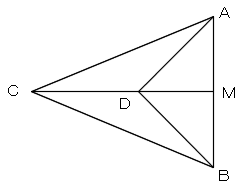
ABの垂直二等分線上で、ABの中点Mから、AMの長さの
1+√2倍の長さ行ったところがCです。
|
No.42785 - 2017/04/13(Thu) 20:32:45 |
| ☆ Re: 2等辺三角形の点座標 / らすかる | | | 私が求めた方法もヨッシーさんが書かれた方法と同じでした。
ABの中点をMとし、MD=MAとなるようにCM上に点Dをとります。
△DBA,△MAD,△MDBは直角二等辺三角形となり、∠DBA=∠DAB=45°です。
∠MAC=∠MBC=90°-22.5°=67.5°なので
∠DAC=∠DBC=67.5°-45°=22.5°、従って
△DACと△DCBは二等辺三角形となりDA=DB=DCです。
よってDC=(√2)DMです。
→AB=(89.073,69.583)-(67.923,101.476)=(21.15,-31.893)
→AM=(1/2)→AB=(10.575,-15.9465)
M=A+→AM=(67.923,101.476)+(10.575,-15.9465)=(78.498,85.5295)
→AM=(10.575,-15.9465)から→MD=(-15.9465,-10.575)なので
→MC=(1+√2)→MD=(-38.4983,-25.5303)
∴C=M+→MC=(78.498,85.5295)+(-38.4983,-25.5303)=(39.9997,59.9992)
検算
√{(39.9997-67.923)^2+(59.9992-101.476)^2}=50.0004
√{(39.9997-89.073)^2+(59.9992-69.583)^2}=50.0004
一般には、A(ax,ay),B(bx,by),等辺の長さがlのとき
d=(ax-bx)^2+(ay-by)^2, r=√(4l^2/d-1) として
C({(bx+ax)+r(by-ay)}/2,{(by+ay)+r(ax-bx)}/2)
となります。
この公式にあてはめて求めると
d=(67.923-89.073)^2+(101.476-69.583)^2=1464.486
r=√(4×50^2/1464.486-1)=2.4142
{(89.073+67.923)+2.4142(69.583-101.476)}/2=39.99996
{(69.583+101.476)+2.4142*(67.923-89.073)}/2=59.99934
∴C(39.99996,59.99934)
# 上の方法では角度だけ使って等辺の長さを使いませんでしたが、
# 下の公式では等辺の長さだけ使って角度は使っていません。
|
No.42786 - 2017/04/13(Thu) 20:54:32 |
| ☆ Re: 2等辺三角形の点座標 / きゅう | | | No.42792 - 2017/04/14(Fri) 05:08:52 |
|