図形を表示できなくて、すみません。
ホームのマークをクリックお願い致します。
灘中の算数で、
「2日目」の「問4」の解き方を教えてください。
「3:4:5」の直角三角形の周りに出来ていく図形達
で特に(2)の答えから、
また「3:4:5」ができることに気づきました。
よろしくお願い致します。
|
No.41823 - 2017/02/08(Wed) 21:32:48
| ☆ Re: 気になった問題 / 関数電卓 | | | とりあえず(1)
△ABC を B を中心に反時計回りに 90°回転させると 赤 に、C を中心に時計回りに 90°回転させると 緑 になる。
図から △BDI=△CEF=6 だから、
六角形 DEFGHI=9+16+25+6×4=74
![]() |
No.41829 - 2017/02/09(Thu) 00:10:55 |
| ☆ Re: 気になった問題 / angel | | | 取り敢えず、この問題の核心だけ。
3,4,5の長さに関係なく、この図のようなことが分かります。
![]() |
No.41830 - 2017/02/09(Thu) 00:12:41 |
| ☆ Re: 気になった問題 / angel | | | ということで、色々三角形と正方形の面積が分かります。
この時点で(1)の答えが出ますね。
![]() |
No.41831 - 2017/02/09(Thu) 00:23:24 |
| ☆ Re: 気になった問題 / angel | | | 後は、残った部分 ( 台形めいた4角形3つ ) を、△ABCの方に寄せてきます。
丁度、N,M、O,J、K,L がくっつくように
( A,G,H、B,D,I、C,E,F もくっつきます )
そうすると、実はくっついた時の境界線が、△ABCの各中線になっていて、元の三角形の4倍拡大になっていることが分かります。
なので、(2)の各長さと、残りの面積も分かる、ということになります。
![]() |
No.41832 - 2017/02/09(Thu) 00:40:27 |
| ☆ Re: 気になった問題 / angel | | | あっと。
AG,ANしか確かめてないのに、なんで全体が4倍拡大と分かるんだ、と思われるかも知れません。
が、これは上の「核心」から分かるようになっています。
Cから引いた△ABCの中線と、EFの長さの比が 1:2 となるのです。
CGは中線の2/3倍、くっつけた後のCK(CL)はEFと同じ長さですから、結局 CG:CK(CL)=1:3
Cに限らず、A,Bでも同じこと、というわけです。
※Aを実際の長さでやってるのは、直接長さが計算しやすかったからです。
|
No.41836 - 2017/02/09(Thu) 01:20:19 |
| ☆ Re: 気になった問題 / √  | | | 関数電卓さん angelさん
有難うございます。
お陰さまで(1)は理解できました。
図の中の、外側の正方形で、
「52」と「73」の求め方が分かりません。
|
No.41837 - 2017/02/09(Thu) 08:59:56 |
| ☆ Re: 気になった問題 / ヨッシー  | | | 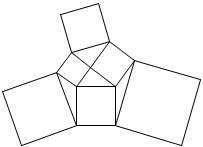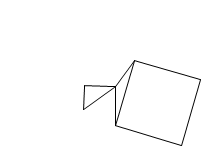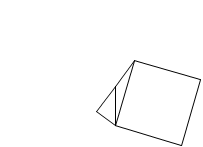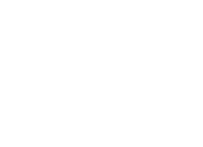
73の方の説明をします。
三平方の定理は、中学受験では普通に使うし、等積変形で示せるので、使えるものと解釈して、
上の図のように直角を挟む2辺が3と8の直角三角形を作ると
その斜辺を1辺とする正方形の面積は
3^2+8^2=73
となります。
52の方も同様に、
4^2+6^2=52
です。
|
No.41839 - 2017/02/09(Thu) 10:59:29 |
| ☆ Re: 気になった問題 / √  | | | ヨッシーさん
有難うございます。
大変よく分かりました!!
ここまでは、スッキリです。
この後が分かりません。
この問題、本当に小学生が解くの? って感じです。
自分のバカさ加減がイヤになってました。
|
No.41840 - 2017/02/09(Thu) 11:41:39 |
| ☆ Re: 気になった問題 / angel | | | ちなみに、私の想定した正方形面積の計算は、中線定理で分かった辺の長さの二乗そのものです。
で、埋まっていないところの面積は、△ABCも含めて、「4倍拡大」ということで16倍の96、で終わりなのですが、どこが不明でしょうか?
※(2)の辺の長さは「4倍拡大」で、単純にAB,BC,CAの4倍です。
要は、この「4倍拡大」に気付けるかどうかで、ヒラメキ命です。
※答えが分かれば良いので、最悪、論理の検証はなしでも解答しちゃいます。
なお、根拠については、ざっくりと、ながら、上に一通り挙げていますので、じっくりご覧ください。
|
No.41844 - 2017/02/09(Thu) 12:45:11 |
| ☆ Re: 気になった問題 / √  | | | angelさん
> 要は、この「4倍拡大」に気付けるかどうかで、ヒラメキ命です。
核心の中線定理が、あまり分かってないのか
命の部分・なぜ4倍になるのかが分かっていません。
(私は基礎が分かっていません)
小学生は、どうやって4倍だと分かるのですか?
|
No.41849 - 2017/02/09(Thu) 15:41:45 |
| ☆ Re: 気になった問題 / √  | | | angelさん
やっと計算が合いました。
有難うございました。
でも小学生には大変難しい計算だと思います。
塾とかでは4倍になると覚え込ませて
しまっているのでしょうか?
|
No.41850 - 2017/02/09(Thu) 16:27:22 |
| ☆ Re: 気になった問題 / angel | | | > でも小学生には大変難しい計算だと思います。
> 塾とかでは4倍になると覚え込ませて
> しまっているのでしょうか?
流石に覚え込ませることはないです。それに4倍というのは流石に計算してます。
というか、いちいち覚えていたらいくらなんでも記憶力がもちません。
で、問題としてはもちろん難しいですが、計算として難しくはないと思います。
実は、「計算して答えが出せる」ということ自体が大きなヒントなのです。あまり変な形だと計算できなくなりますから。
つまり、図のように台形っぽい四角形を寄せた時にできる三角形、これが元の三角形の相似形 ( 拡大 ) ではないか、という推理です。
※受験算数では相似は定番です。
で、私の場合は直角三角形に由来する性質から、中線の存在に気付きました。中線を3本集めればできるのは重心です。つまり、重心を中心とした拡大であろうと。
図の中線と上の正方形の長さは簡単に出ます。
ここから、No.41832で説明したAG=5/3,AN=5 につながって、「4倍」と。
拡大 ( 相似 ) の根拠はある意味後付けなのです。
![]() |
No.41864 - 2017/02/09(Thu) 21:27:41 |
| ☆ Re: 気になった問題 / √  | | | angelさん
有難うございます。
中学受験の小学生は、重心は2:1の内分点であることも
知っているのですね。
私は、それさえも忘れていた状態だったので、
5/3cmという数字が、どこから出てくるのかさえ
分かりませんでした。
今の小学生はスゴイ!
|
No.41876 - 2017/02/10(Fri) 13:26:22 |
|


