x(2π-t)=x(t)かつy(2π-t)=-y(t)という関係が成り立つとき、tが0<t<2πを変化するとき、(x(t),y(t))の描く図形はtが0<t<πを変化するときに描いたものとx軸対称な図形を逆にたどったものである。
上記のような記述があるのですが、この部分の意味がわかりません。なぜこのようなことがいえるのでしょうか。教えてください。よろしくお願いします。
|
No.38383 - 2016/08/04(Thu) 14:11:36
| ☆ Re: グラフの対称性 / ヨッシー  | | | イメージ的には、
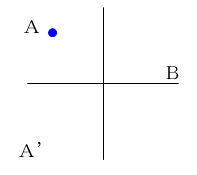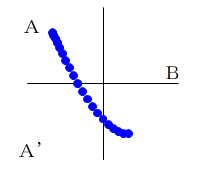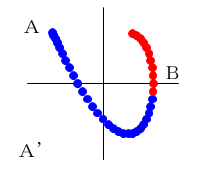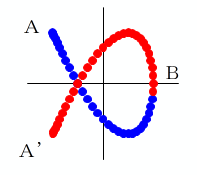
tが0→πまで動いた時に描く図形(青:A〜B)があります。
t=π のとき y(π)=−y(π) より、y(π)=0 なので、
この図形は必ずB(x(π), 0) を通ります。
図形(青:A〜B) をx軸に対称に折り返した図形(赤:B〜A’)を考えます。
A’はAとx軸対称な点です。
tをπ→2πと動かしたとき、点(x(t),y(t))は、BからA’をたどります。
示すには、(x(t),y(t)) と (x(2π−t),y(2π−t)) がx軸に対して
対象になることを言えば良いのですが、定義から一目瞭然です。
|
No.38388 - 2016/08/04(Thu) 16:51:03 |
| ☆ Re: グラフの対称性 / るり | | | 回答ありがとうございます。
(x(2π-t),y(2π-t))と(x(t),y(t))がx軸対称になるのはわかりました。
でも0<t<πとπ<t<2πで対称になるというところがどうもよくわからないです。どうして0<t<πの範囲だけで考えて、それをx軸対称すればいいんでしょうか?
|
No.38418 - 2016/08/05(Fri) 15:14:41 |
| ☆ Re: グラフの対称性 / ヨッシー  | | | 連続値だとイメージしにくいので、
x(200−t)=x(t) かつ y(200−t)=−y(t) のとき、
t=0,1,2,… 200 を考えます。
さらに、(x(200−t),y(200−t)) と (x(t),y(t)) がx軸対称ということまでわかっているので、
(x(0), y(0)) と (x(200), y(200)) はx軸対称
(x(1), y(1)) と (x(199), y(1990)) はx軸対称
(x(2), y(2)) と (x(198), y(198)) はx軸対称
・・・・・
(x(98), y(98)) と (x(102), y(102)) はx軸対称
(x(99), y(99)) と (x(101), y(101)) はx軸対称
(x(100), y(100)) は (0, 0)
が言えますので、t=100〜200 は、t=0〜100 の経路を
x軸対称に移動して、逆から(t=100 から 0 に向けて)たどった軌跡上を移動します。
なぜ、t=100 で折り返すかというと、
200−t と t は、100 に対して対称だからです。
(元の問題でいうと、2π−t と t はπに対して対称)
|
No.38419 - 2016/08/05(Fri) 16:05:13 |
| ☆ Re: グラフの対称性 / るり | | | とてもわかりやすかったです。
ありがとうございました。
|
No.38427 - 2016/08/05(Fri) 21:56:54 |
|
