問題は
(1)曲線C1:y=cosxと曲線C2=sin2xを考える。
区間-π/2≦x≦π/2における曲線C1と曲線C2の3つの共有点のx座標の小さい方から順にx1,x2,x3とする。このとき区間x1≦x≦x2において2曲線C1,C2によって囲まれた部分の面積は【1】である。また区間x2≦x≦x3において2曲線C1,C2によって囲まれた部分の面積は【2】である。
(2)曲線C:y=ax+e^x(aは正の定数)を考える。
曲線Cとx軸、y軸および直線x=1で囲まれた図形をDとする。
図形Dの面積がeであるとき、a=【3】である。また、図形Dをx軸の周りに1回転してできる回転体の体積は【4】である。
答えは【1】3/2、【2】5/4、【3】2、【4】π{(3/2)e-1}
だそうですが、計算で至る過程がわかりません。(答えがあっているかどうかもわかりません)
多くて申し訳ございませんが、詳しく説明をお願いします。
|
No.35762 - 2016/02/14(Sun) 22:09:36
| ☆ Re: 積分?です / ヨッシー  | | | 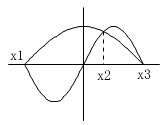
(1)
x1=−π/2, x2=π/6, x3=π/2 であるので、
∫[x1〜x2]{cosx−sin2x}dx=9/4 ・・・【1】
∫[x2〜x3]{sin2x−cosx}dx=1/4 ・・・【2】
(2)
D=∫[0〜1](ax+e^x)dx=a/2+e−1
これがeに等しいので、
a=2 ・・・【3】
このとき、求める体積をVとすると
V=π∫[0〜1](2x+e^x)^2dx
=π∫[0〜1](4x^2+4xe^x+e^(2x))dx
∫[0〜1](4x^2+e^(2x))dx=5/6+(1/2)e^2
∫[0〜1]4xe^xdx=∫[0〜1]4x(e^x)'dx
=[4xe^x][0〜1]−∫[0〜1]4e^xdx=4
よって、
V=π(29/6+e^2/2) ・・・【4】
|
No.35773 - 2016/02/15(Mon) 13:06:08 |
|