三角形OABにおいてある点HがsOA+tOBと表され、s+t>1が成り立つ時、どうしてHは三角形OABの外部にあると言えるのでしょうか。
|
No.83534 - 2022/10/03(Mon) 21:39:32
| ☆ Re: ベクトル / IT | | | 対偶を考えると良いと思います。
H=sOA+tOBが三角形OABの内部(辺を含む)にあるとき
s+t がどうなるか図を描いて確認してみると良いです。
(H≠OのときはOHとABとの交点をPとします。)
|
No.83535 - 2022/10/03(Mon) 21:55:29 |
| ☆ Re: ベクトル / ヨッシー  | | | こういう考え方も出来ます。
OA=(1,0)、OB=(0,1) とすると、
sOA+tOB
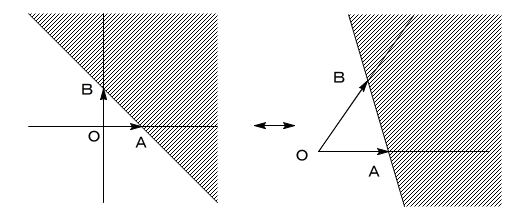
は、点(s,t)を表し、s+t>1 は、x+y>1 に対応します。
OAとOBが直行していなくても、また、
OA、OB の大きさが1でなくても、
座標としての相対的な位置関係は変わらないので、
左と右の図は同じことを表していると言えます。
|
No.83536 - 2022/10/03(Mon) 22:12:11 |
| ☆ Re: ベクトル / けんけんぱ | | | とりあえず、内分を理解し、s+t=1のときは直線AB上の点になることを理解することが先決だと思います。
そのあとで、s+t<1のときやs+t>1のときを考えるのが良いと思います。
|
No.83537 - 2022/10/03(Mon) 22:51:49 |
| ☆ Re: ベクトル / ast | | | > Hは三角形OABの外部にあると言える
というのは少し不正確で, ヨッシーさんの提示された図を見るとわかると思いますが, 点 H は "(3点 O,A,B を含む) 平面を直線 AB で二つに分割したときの点 O を含まない側の領域" 上にあります.
# 三角形 OAB の外部よりも限定的な領域にあるということです.
# (まあ, "少なくとも三角形 OAB の内部にない" ことを言うのに十分な条件ではありますが.)
より具体的に: s+t=a (a>0, a≠1) のとき, 点 A', B' を OA'=aOA, OB'=aOB で定める (つまり, 三角形 OA'B' は三角形 OAB に対して相似比 a の相似三角形) と, s'=s/a, t'=t/a とすれば
OH=sOA+tOB=(s/a)(aOA)=(t/a)(aOB)=s'OA'+t'OB' (s'+t'=1)
となり, けんけんばさんがすでにご指摘のように「s+t=1 ⇔ 直線上にある」という話に帰着されます.
# s+t=1 のとき, s=1-t と書けて, t に依存して動く動点 P[t] を
# OP[t]=(1-t)OA + tOB = OA + tAB
# ととると, その軌跡は二点 P[0]=A, P[1]=B を通り, 方向ベクトルが AB で与えられる直線になります.
# とくに 0≤t≤1 の範囲は線分 AB になります.
そうすると
[i] 点 H が直線 A'B' 上にあること,
[ii] 直線 A'B' が直線 AB に平行であること
(直線 A'B' のある場所は,
a<1 のとき直線 AB に対して点 O のある側,
a>1 のとき AB に対して点 O と反対側)
なので, a>1 の範囲で a を任意に動かすとき直線 A'B' の掃く範囲が H の存在領域であるということができます.
|
No.83538 - 2022/10/04(Tue) 02:10:23 |
|
