3点a(3,0,0),b(0,t,0),c(0,0,1)を通る平面αと5点p(0,0,2),q(2,0,0),r(0,2,0),s(ー2,0,0),t(0,ー2,0)が頂点の四角錐Vがある.(t≧2)
(1)Vをαで切った切り口の面積S(t)を求めよ.
(2)S(t)の最大値を求めよ.
よろしくお願いします!
|
No.31812 - 2015/06/19(Fri) 22:18:58
| ☆ Re: 空間座標 / ヨッシー  | | | 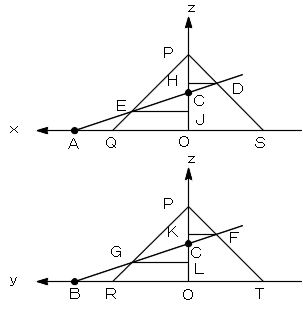
zx平面において、△QPS と直線ACを考えます。
ACとPS,PQとの交点をD,Eとし、D,Eからz軸に下ろした垂線の足をH,J
とします。
△ACO∝△DCH であり、AO:OC=3:1 なので、
CH=DH/3
また
PH=DH
であるので、
CH=PC/4=1/4
よって、Dの座標は(-3/4, 0, 5/4)
△ECJ∝△ACO であり、AO:OC=3:1 なので、
CJ=EJ/3
また
EJ=PJ
であるので
CJ=PC/2=1/2
よって、Eの座標は(3/2, 0, 1/2)
同様にyz平面において、△RPT と直線BCを考えます。
BCとPT,PRとの交点をF,G とし、F、Gからz軸に下ろした垂線の足をK,L
とします。
上と同様に計算して
Fの座標(0, -t/(t+1), (t+2)/(t+1))
Gの座標(0, t/(t-1), (t-2)/(t-1))
ここで、
DE=(3/4, 0, -3/4)
FG=(0, 2t/(t^2-1), -2t/(t^2-1))
この2つのベクトルが作る三角形がSと等しくなります。
DE=3√2/4
FG=2√2t/(t^2-1)
DE・FG=3t/2(t^2-1)
より、DEとFGのなす角をθとすると
cosθ=1/2
よって
sinθ=√3/2
S(t)=(1/2)(3√2/4){2√2t/(t^2-1)}(√3/2)
=3√3t/4(t^2-1)
T(t)=t/(t^2-1) とおきます。
Tをtで微分して
T'(t)=-(t^2+1)/(t^2-1)^2
よって、T(t) は単調減少関数であり、最大値はt=3 のとき
このとき
S(3)=9√3/32
|
No.31814 - 2015/06/20(Sat) 00:24:26 |
|
