塾の課題です。どなたかお願いします。
空間内に1辺の長さが1の立方体OABC-DEFGと平面Hがあり、両者はOのみを共有している。
このとき以下の問いに答えよ。
(1)Oを通り↑nに垂直な平面と点Pとの距離をdとする。
d=|↑n・↑OP|/|↑n|を示せ。
(2)点A,B,C,D,E,F,GからHまでの距離の和をSとする。
Sの最大値を求めよ。
(3)点A,B,C,D,E,F,GからHまでの距離の2乗の和をTとする。
Tのさを求めよ。
|
No.31760 - 2015/06/15(Mon) 23:34:35
| ☆ Re: / 陽 | | | No.31761 - 2015/06/15(Mon) 23:35:02 |
| ☆ Re: / ヨッシー  | | | 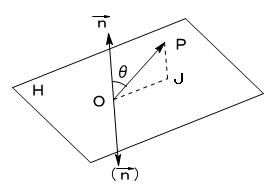
(1)
点Pから平面Hに下ろした垂線の足をJとすると、PJが求める距離となります。
n と OP のなす角またはその補角(180°からその角を引いた角度)のうち
0°以上 π/2 以下の範囲にある方をθとすると、
図において、求める距離PJは、
PJ=OPcosθ
と書けます。
一方、
|n・OP|=|n||OP|cosθ
より、
d=|n・OP|/|n|
=|OP|cosθ
となり、dが求める距離であることは明らかです。
(2)
a=OA, c=OC, d=OD とおきます。
各点A〜G から平面Hまでの距離を d[A]〜d[G] とします。
立方体と平面Hは点Oのみを共有するので、nを点Oから立方体の存在する側に取れば、
(1) の絶対値は必要なく
d=n・OP/|n|
と書けます。
よって、
d[A]=n・OA/|n|
d[B]=n・OB/|n|
・・・
d[G]=n・OG/|n|
より、
S=n・(OA+OB+・・・+OG)/|n|
=4n・(a+c+d)/|n|
=4n・OF/|n|
となり、n//OF すなわち、OFが平面Hに垂直なとき
Sは最大となります。このとき、
S=4|n|・|OF|/|n|=4OF=4√3
(3)
nとOA、OC、OD のなす角をα、β、γ とします。
このとき、
cos^2α+cos^2β+cos^2γ=1
が成り立ちます。
d[A]=n・OA/|n|=OAcosα=cosα
d[A]^2=cos^2α
d[B]=n・OB/|n|
=(n・a+n・c)/|n|
=OAcosα+OCcosβ=cosα+cosβ
d[B]^2=cos^2α+cos^2β+2cosαcosβ
・・・
これらを計算して
T=4(cos^2α+cos^2β+cos^2γ)+4(cosαcosβ+cosβcosγ+cosγcosα)
=8(cos^2α+cos^2β+cos^2γ)−4(cos^2α+cos^2β+cos^2γ)+4(cosαcosβ+cosβcosγ+cosγcosα)
=8−2{(cosα−cosβ)^2+(cosβ−cosγ)^2+(cosγ−cosα)^2}
よって、Tは、cosα=cosβ=cosγ のとき最大値8を取ります。
|
No.31772 - 2015/06/17(Wed) 09:42:33 |
|