xy平面上に存在する三点A,B,Cは以下の条件を満たす
点Aはx軸上正方向の部分、点Bはy軸上正方向の部分、点Cは原点中心半径1の円周上に存在する
この時、三角形ABCが正三角形をとるときの面積のとれる範囲を求めよ
上記の問題に全く歯が立ちませんでした。どれかの値を固定してみても、そこから進みません。
どのように解けば良いのでしょうか?
宜しくお願いします
|
No.31296 - 2015/04/30(Thu) 22:22:00
| ☆ Re: 正三角形の面積 高校三年生 / とむとむ | | | 追記です
A(a,0) B(0,b)とおき、ベクトルの回転を利用して点C
の座標を出した後、x^2+y^2=1に代入し、a^2+b^2±(√3)=1までは出せました
面積はa^2+b^2の範囲が分かれば出せると思うのですが、ここからが出せません
どうすれば良いでしょうか?
|
No.31297 - 2015/04/30(Thu) 22:28:38 |
| ☆ Re: 正三角形の面積 高校三年生 / 歌声喫茶 | | | 面積の範囲ということはつまり辺の長さの範囲が分かればいいので、あとどうせ座標平面が絡むので辺の長さの2乗を考えたほうが楽だろうなあと最初に考えます。これが「面積はa^2+b^2の範囲が分かれば…」の部分ですね。
そして、せっかくの「原点中心半径1の円周上」という条件なので扱いやすいまま扱うといいです。つまり、C(cosθ,sinθ)とおけば、a,b,θの式で条件を表せて、そうすればa^2+b^2は範囲を求めやすい形で表せます。なお、θの範囲にも留意してください。
|
No.31298 - 2015/04/30(Thu) 23:36:49 |
| ☆ Re: 正三角形の面積 高校三年生 / とむとむ | | | C(cosθ,sinθ)と置いて解いて見ようとしましたが、上手くいきません。正三角形の成立条件の際、回転する方向によって±、θの範囲共に複雑になります
具体的な計算過程を教えていただきたいです
|
No.31301 - 2015/05/01(Fri) 00:35:14 |
| ☆ Re: 正三角形の面積 高校三年生 / 歌声喫茶 | | | それなら一度にやろうとせずにそれぞれの方向の場合を別々に考えればよいのでは?
|
No.31302 - 2015/05/01(Fri) 11:03:51 |
| ☆ Re: 正三角形の面積 高校三年生 / とむとむ | | | 三角関数が上手く行かないので下記のようにやってみました。不備がありましたら教えていただきたいです
正の数a、bに対しA:(a,0)、B:(0,b) とするとき、
線分ABを一辺にもつ正三角形の第3の頂点が円x^2+y^2=1上にあるための条件として
実正数a,bはa^2+b^2±(√3)ab=1 を満たす
a,bが実数である条件は (a+b)^2≧0 かつ (a-b)^2≧0 なので、
ab=±(1-a^2-b^2)/√3 を a^2+b^2≧2abの右辺に代入すれば
2/(2+√3)≦a^2+b^2<1 または 1<a^2+b^2≦2/(2-√3)
最初の不等式の等号は a^2=b^2=1/(2+√3)、後の不等式の等号は a^2=b^2=1/(2-√3)
の時に起こります。
正三角の一辺の長さは √(a^2+b^2) なので、以上を総合して正三角形ABCの面積を得る
略解ですが、このような感じです。どうでしょうか?
|
No.31304 - 2015/05/01(Fri) 23:50:56 |
| ☆ Re: 正三角形の面積 高校三年生 / 歌声喫茶 | | | あ、おおむねそんな感じです。代数で押してもあまり面倒にはならないんですね。
a,bの関係式から楕円を見抜くという手もあります。…実用的かはさておいて。
|
No.31308 - 2015/05/02(Sat) 09:24:18 |
| ☆ Re: 正三角形の面積 高校三年生 / ヨッシー  | | | 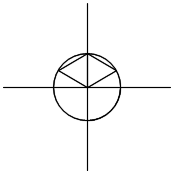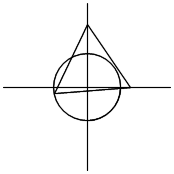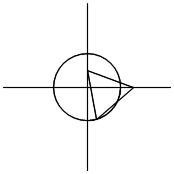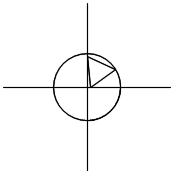
一応、参考に。
|
No.31309 - 2015/05/02(Sat) 11:18:26 |
| ☆ Re: 正三角形の面積 高校三年生 / とむとむ | | | 歌声喫茶さん、ヨッシーさん有り難うございました
しかし、もうひとつだけ疑問があります
自分で解答しといて馬鹿みたいな内容なのですが、a,bが正であることは自分で設定しただけで、条件を満たすとき本当にa,bが正であるか示せていない気がします
平気なのでしょうか?
|
No.31310 - 2015/05/02(Sat) 12:46:38 |
| ☆ Re: 正三角形の面積 高校三年生 / 歌声喫茶 | | | >a^2+b^2±(√3)ab=1
これをa,bのうち少なくとも1つが負であるような値の組が満たしたとすると、その負であるものを-1倍したものもこの式を当然満たします(2乗と復号ですから)。略解という事で細かいとこには触れませんでしたが、きちんと答案に起こすなら当然その辺りは詰めておくべきでしょう。
原点についての対称性を考えてみれば、実はa,bが正というのはa,b≠0ぐらいの意味しか持ちません…というのは、言われてみればそりゃそうだという気がしますよね。
|
No.31311 - 2015/05/02(Sat) 15:16:12 |
| ☆ Re: 正三角形の面積 高校三年生 / とむとむ | | | 遅くなり申し訳ありません
無事解決出来ました
有り難うございました
|
No.31320 - 2015/05/03(Sun) 10:50:07 |
|
