自然数の列を 1,2 / 3,4,5,6 / 7,8,9,10,11,12 / ..... のような群数に分ける ?@第n群の最初の項 ?A第n群の項の総和 をお願いします。
|
No.15564 - 2011/10/22(Sat) 19:56:58
| ☆ Re: 群数列 / ヨッシー  | | | 群数列の場合、まず、どういう分け方をしているかを
ちゃんと理解しているかがポイントになります。
どういうふうに分けていると思いますか?
第10群の数列を書き並べることは出来ますか?
第100群の最初の数と、最後の数を答えられますか?
|
No.15565 - 2011/10/22(Sat) 20:36:15 |
| ☆ Re: 群数列 / ポパイ | | | 2の倍数でわけてありますよね。
第10群列は 91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110
第100群列の最初と最後はわかりません。
|
No.15566 - 2011/10/22(Sat) 21:51:33 |
| ☆ Re: 群数列 / ヨッシー  | | | そうですね。
第1群は2個、第2群は4個、・・・第10群は20個、・・・第n群は2n個
の数字があります。
第9群までで、
2+4+6+・・・+18
=2(1+2+3+・・・+9)
=2×9×10÷2=90(個)
の数字が使われていますので、第10群はその次の91から
2×10×11÷2=110
までの20項になります。
同様に第99群までは
2×99×100÷2=9900
まで、使われているので、第100群は 9901 から
2×100×101÷2=10100 までの200項です。
※1+2+3+・・・+n=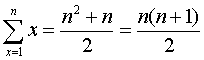
を使っています。
さて、本問ですが、
(1)第n群の最初の項
第n-1群までで
2×(n-1)×n÷2=n(n-1) (個)
の数字を使っているので、第n群の最初の項は
n(n-1)+1
です。
(2)第n群の項の総和
第n群の最後の項は
2×n×(n+1)÷2=n(n+1)
で、第n群は n(n-1)+1 から n(n+1) までの2n個となります。
(等差数列の和)={(初項)+(末項)}×(項数)÷2
より
{n(n-1)+1+n(n+1)}×2n÷2=n(2n^2+1)
となります。
|
No.15571 - 2011/10/23(Sun) 08:15:50 |
| ☆ Re: 群数列 / ポパイ | | | ありがとうございました。
この解答をもとにもう一度解いてみます。
|
No.15578 - 2011/10/23(Sun) 20:12:59 |
|



