直線L_1,L_2,L_3,...L_n (nは正の整数)が、
一点で交わっているとする。その点を原点とおく。
ここで、以下の条件を考える。
(i): 任意の直線に隣り合う直線とのなす角は常に2π/nである。
以下の問いに答えよ。
(1) ある直線L_kとL_m (k,m = 1,2,3,..,n)をそれぞれ中心軸とする半径aの円柱の共通部分の体積V_(k,m)を求めよ。
(2) L_1,L_2,L_3,...,L_nをそれぞれ中心軸とする半径aの円柱の共通部分の領域をDとする。
Dの不連続点と極値をすべて求めよ。
(3) 領域Dの体積を求めよ。
わからないです、教えてください。
|
No.76602 - 2021/07/12(Mon) 10:16:08
| ☆ Re: / 編入受験生 | | | No.76603 - 2021/07/12(Mon) 10:17:06 |
| ☆ Re: / 高校三年生 | | | 各直線に垂直な直線を含む平面で切った断面が、円から楕円へ、
そしてまた、楕円から円へと周期的に変化する立体になりそうですね。
どうやって体積を導出するんだろう?
|
No.76609 - 2021/07/12(Mon) 14:23:16 |
| ☆ Re: / ヨッシー  | | | 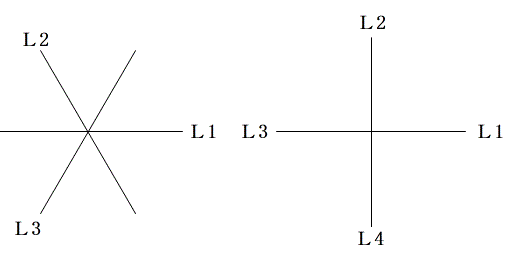
確認ですが、n=3、n=4 の時の図は上の通りでいいでしょうか?
n=3のときは、隣り合う直線とのなす角は π/3 になりません。
n=4のときは、L_1とL_3、L_2とL_4 は重なります。
角度は2π/4=π/2 となり条件は満たします。
nが偶数とか奇数とかの制限はありませんか?
もしくは、上の解釈が違っているか。
|
No.76610 - 2021/07/12(Mon) 14:43:59 |
| ☆ Re: / 編入受験生 | | | >
> 確認ですが、n=3、n=4 の時の図は上の通りでいいでしょうか?
> n=3のときは、隣り合う直線とのなす角は π/3 になりません。
> n=4のときは、L_1とL_3、L_2とL_4 は重なります。
> 角度は2π/4=π/2 となり条件は満たします。
>
> nが偶数とか奇数とかの制限はありませんか?
> もしくは、上の解釈が違っているか。
すみません、なす角はπ/nです。
間違えてました。
|
No.76611 - 2021/07/12(Mon) 15:58:24 |
| ☆ Re: / 関数電卓 | | | こちら の問題を追求しておられるのですね。
前回は軸に垂直な断面で切って give up しましたが,軸がある平面に平行に切断する方法もありそうです。根気が続くところまでやってみます。
|
No.76614 - 2021/07/12(Mon) 18:34:32 |
| ☆ Re: / 黄桃 | | | (2)は置いときます。
細かい計算は苦手なので方針だけ。ガードナーの数学ゲームにあった解法です。
直線がある平面と平行な平面で切った時、求める図形の切断面と、共通部分の内接球(=半径aの球)の断面(=円)との比は一定なので、(カバリエリの原理より面積比は内接球との体積比と等しいので)積分計算せずに体積が求まりそうです。
(3)の方が対称性があるので計算は楽そうです。(3)の答は半径1の円に外接する正n角形の面積をS[n]とすれば、(4/3)*S[n]*a^3 となるのでしょう。
|
No.76636 - 2021/07/13(Tue) 00:59:07 |
|
